Social Returns to Productivity Growth

Published: July 03, 2022 | by Tom Davidson

Intro

At Open Philanthropy we aim to do the most good possible with our grantmaking. Historically, economic growth has had huge social benefits, lifting billions out of poverty and improving health outcomes around the world. This leads some to argue that accelerating economic growth, or at least productivity growth,^[1]If environmental constraints require that we reduce our use of various natural resources, productivity growth can allow us to maintain our standards of living while using fewer of these scarce inputs. should be a major philanthropic and social priority going forward.^[2]For example, in Stubborn Attachments Tyler Cowen argues that the best way to improve the long-run future is to maximize the rate of sustainable economic growth. A similar view is held by many involved in Progress Studies, an intellectual movement that aims to understand and accelerate … Continue reading

In this report, I describe a model that helps assess this view and inform our Global Health and Wellbeing (GHW) grantmaking. Specifically, I focus on quantitatively estimating the social returns to directly funding research and development (R&D), in a relatively simple/tractable model. I focus on R&D spending because it seems like a particularly promising way to accelerate productivity growth, but I think broadly similar conclusions would apply to other innovative activities.

Having a reliable estimate of the social returns to innovation would allow us to quantitatively compare it to other potential philanthropic activities like cash transfers to the global poor or public health interventions that extend life, and then accordingly allocate our total funding in the optimal fashion. However, we’re not sure how much weight to put on this particular estimate given the simplifications and assumptions involved.

In brief, I find that:

In a highly stylized calculation, the social returns to marginal R&D are high, but typically not as high as the returns in some other areas we’re interested in (e.g. cash transfers to those in absolute poverty). Measured in our units of impact (where “1X” is giving cash to someone earning $50k/year) I estimate the cost effectiveness of funding R&D is 45X. This is 45% the ROI from giving cash to someone earning $500/year, and 4.5% the GHW bar for funding. More.
- This is an estimate of the average returns to R&D, but the best R&D projects might have higher returns. In addition, leveraged opportunities to increase the amount of R&D — like advocating for a more liberal approach to high-skill immigration — could have significantly higher returns. More.
Returns to R&D were plausibly much higher in the past. This is because R&D was much more neglected, and because of feedback loops where R&D increased the amount of R&D occurring at later times. More.
The stylized estimate has many important limitations, and is not an all-things-considered estimate of the social returns to R&D. For example:
- It omits potential downsides to R&D, e.g. increasing global catastrophic risks. For certain types of R&D, these downsides may significantly outweigh the benefits. This is a very significant limitation of the estimate. More.
- It focuses on a specific scenario in which population growth stagnates and historical rates of returns to R&D continue to apply. In this scenario, productivity growth eventually stagnates. While this is arguably the most popular model of the future, it is not the only plausible one, and I discuss how placing weight on alternative scenarios would change the bottom line. More.
  - One such scenario is that R&D today brings forward the development of a future technology, like advanced AI, that accelerates R&D progress much more than past technologies. This could significantly increase the returns to R&D. But conditional on such a scenario Open Philanthropy sees a stronger case for reducing long-term risks from this future technology than accelerating its development. More.
Overall, the model gives us a new stylized value for the ROI of abstract marginal R&D spending that we may use in Global Health and Wellbeing cause prioritization work, though we have substantial uncertainty about how much weight to put on it given all of the assumptions and limitations. The stylized value we get out does make us think that some causes aimed at accelerating overall innovation, like science policy or high-skill immigration advocacy, would likely pencil out as above our GHW bar, but it also leaves us relatively skeptical of arguments that accelerating innovation should be the primary social priority going forward. More.

My estimate of the social returns to R&D

I draw heavily on the methodology of Jones and Summers (2020). I won’t explain their model in full, but the basic idea is to estimate two things:

How much would a little bit of extra R&D today increase people’s incomes into the future, holding fixed the amount of R&D conducted at later times?^[3]An example of an intervention causing a temporary boost in R&D activity would be to fund some researchers for a limited period of time. Another example would be to bring forward in time a policy change that permanently increases the number of researchers.
How much welfare is produced by this increase in income?

For part 1, I use economic growth models that connect R&D investments with subsequent productivity growth. For part 2, I use a simple log-utility model: welfare = k + m*log(income).^[4]Three comments on the log-utility model. First, the results are the same whatever the values of the constants k and m. Second, I do a sensitivity analysis of the consequences of different utility functions; if the diminishing returns to income are steeper than log, this favours cash transfers more … Continue reading This log-utility model has two implications that I will use:

Increasing someone’s income by 10% has the same welfare effect whatever their initial income.
Increasing one person’s income by 10% has roughly the same welfare effect as increasing ten people’s incomes by 1%, or as increasing 100 people’s incomes by 0.1%, or 1000 people’s incomes by 0.01%.^[5]log(110) – log(100) ~= 10*[log(101) – log(100)] ~= 100*[log(100.1) – log(100)] ~= 1000*[log(100.01) – log(100)].

Toy Example

Here’s a toy example to roughly demonstrate how I calculate the social returns to R&D, and how this can be compared with cash transfers to people in global poverty.

Let’s estimate the welfare benefits of spending $20 billion on R&D.

Total global R&D spend is $2 trillion per year. This produces frontier productivity growth of 1% per year.
$20 billion would increase global R&D spend by a fraction of 1/100 for 1 year. So in that year, rather than 1% productivity growth we’d expect to have 1.01% productivity growth.^[6]More realistically, there will be a lag before productivity benefits are felt. Currently I don’t model this lag because it wouldn’t affect the results by much. I use a discount of 0.2%; so a 50 year lag would reduce the returns to R&D by ~10%.
In subsequent years, everyone’s incomes will be 0.01% higher because of the extra money spent on R&D in that one year.
The benefit in each year is equal to (number of people alive) * (value of raising someone’s income by 0.01% for one year).
Let’s ignore the benefits after 50 years, as a rough way to incorporate a discount rate.
For simplicity, let’s assume the number of people alive is constant at 8 billion.

These assumptions imply that:

Social returns to $20 billion on R&D
= (number of people alive) * (value of raising someone’s income by 0.01% for one year) * (years of benefit)

= 8 billion * (value of raising someone’s income by 0.01% for one year) * 50

= 400 billion * (value of raising someone’s income by 0.01% for one year)

= 400 million * (value of raising someone’s income by 10% for one year)

This last line follows from the log-utility model: increasing 1000 people’s incomes by 0.01% has the same welfare effect as increasing one person’s income by 10%.

The conclusion is that spending $20 billion on R&D has the same welfare benefit as increasing the incomes of 400 million people by 10% each. (In fact it would increase many more people’s incomes by a much smaller amount; the log-utility model allows us to express the welfare benefit in this way.)

An alternative altruistic intervention is simply to transfer cash directly to the global poor.^[7]GiveDirectly implements this intervention. Note, I use simplified numbers in this post that don’t exactly match GiveDirectly’s cost effectiveness, and I believe GiveDirectly is somewhat more impactful than the numbers I use imply. For someone living below the international poverty line on $500/year, $50 raises their income by 10% for one year. With $20 billion, you could do this 20 billion / 50 = 400 million times. The total benefit would equal 400 million * (value of raising someone’s income by 10% for one year).

In this toy example, the social returns to R&D exactly equals that from cash transfers. As we’ll see below, a more realistic calculation seems to favour cash transfers over R&D.

The main factor favouring R&D is its potential to help so many people as technological innovations spread across the world. The main factor favouring cash transfers is that even a small amount of money can significantly improve the lives of people in poverty.

A more realistic calculation

The actual calculation of the social returns to R&D differs from this toy example in a few important ways. This table summarises these differences, and their effects on the social returns to R&D. Some of the differences interact in complex ways, so there’s no simple way to describe their quantitative effect.

Difference from the toy example	Effect on the social returns to R&D compared to the toy example
I count benefits over a longer period of time	Increase
I recognise that ideas are getting harder to find	Decrease
I use UN population projections	Small increase
I think that some people might not benefit from frontier technological progress.	Decrease, 0.7X
I only give R&D partial credit for productivity growth	Decrease, 0.4X
I assume diminishing returns to adding more researchers within any given year	Small decrease
I incorporate capital deepening: higher productivity → more machines → higher incomes.	Increase, 1.5X
Total, combining all the above differences	Decrease, 0.45X

Let’s discuss each difference in more detail.

I count benefits over a longer period of time. We should value improving someone’s life equally whether they live now or in 500 years time.^[8]Note, rising incomes mean we don’t value adding an equal dollar amount to people’s incomes the same amount through time. We value a dollar more today because people today are poorer than they will be in the future. I use a small pure time discount of 0.2%, representing the possibility that a major disruption (e.g. extinction) prevents the welfare benefits of R&D from occurring at all. This small discount pushes towards placing a higher value on R&D, compared to the toy example.

I recognise that ideas are getting harder to find. Let’s say that R&D makes progress by coming up with new ideas, and define an ‘idea’ so that each new idea raises productivity by 1%. It turns out that there’s good evidence that it takes more research effort to find new ideas than it used to.^[9] During the 20th century, the number of researchers grew exponentially, but productivity growth did not increase (in fact it decreased slightly). If R&D is responsible for the productivity growth, then more research effort is required to achieve each subsequent 1% gain in productivity. One plausible explanation is that the most obvious ideas are discovered first, so that over time increasingly difficult ones remain. Another explanation is that researchers must spend increasingly long studying before they’re able to contribute to their fields.

Importantly, ideas are getting harder to find despite researchers having better tools (e.g. the internet) to aid their research today than in the past. Even with these improved tools, it still takes more research effort to find new ideas than it used to.

How does this dynamic affect social returns to R&D? In the toy example, the extra R&D caused everyone’s incomes to be 0.01% higher forever. It turns out that once you incorporate ‘ideas getting harder to find’, this is no longer true. The % income benefit shrinks over time and approaches 0%.^[10]Note: this does not mean that the absolute $ increase in incomes shrinks over time. It may decline, stay constant or increase, depending on the rate at which ideas are getting harder to find. Technically, if the “fishing out” parameter $ \phi $ > 0, then the absolute $ benefit increases … Continue reading

This is shown in the diagram below, which compares the total factor productivity (TFP) in a world without any intervention (orange) and a world where an intervention temporarily boosts R&D activity (blue). Note: the y-axis is log, so the gap between the lines represents the % difference in TFP, not the absolute difference.

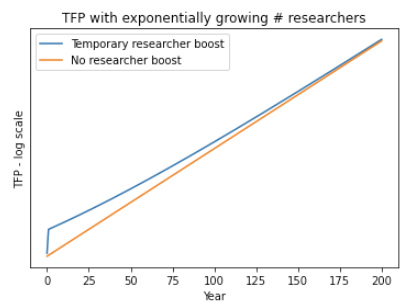
The initial % increase declines towards 0% over time. This dynamic decreases the social returns to R&D, compared to the toy example.

Why does the % productivity increase decline in this way? Essentially, the initial extra R&D “steals” easier to find ideas from future years, making future research less productive (see footnote for more detail).^[11]The key point is as follows: when ideas are getting harder to find, the number of new ideas found with a marginal researcher-year is roughly proportional to 1 / (total researcher-years so far). So if the 100th researcher-year finds 1/100 new ideas, the 200th researcher-year will find only 1/200 new … Continue reading

How quickly are ideas getting harder to find? I use an estimate from Bloom et al (2020), which looks at how research efforts translated into TFP growth in the US from 1930 to 2015. The implication is that each time TFP doubles, it becomes ~5X as hard to find a new idea.^[12]Mathematically, in the semi-endogenous growth model the effort needed to find a new idea is proportional to TFP^($ \phi $ – 1), where $ \phi $ is the parameter controlling how quickly ideas are getting harder to find. I use $ \phi $ = -1.4, so every time TFP doubles the effort needed to … Continue reading

As a result of this dynamic, most of the benefits of today’s R&D occur in the first 100 years despite the small discount rate.

I use UN population projections. When estimating the number of future beneficiaries for today’s R&D, I used the UN population projections which forecast that the global population will rise to around 11 billion by 2100 and then remain at that level.^[13]In the long run, there are reasons to think population will fall (fertility rates in developed countries), reasons to think it might increase (relating to biological and cultural evolution), and no compelling reason to think it will stay exactly the same. Still, this feels like a fair … Continue reading These projections also inform my estimate of the amount of R&D that will be done in each year in the future. This contrasts with formal economic models in which the population is typically assumed to be constant or increasing exponentially.

The toy example assumed that the population would remain at 8 billion. Compared to this, using UN population projections increases the number of beneficiaries and so increases the returns to R&D.

I think that some people may never benefit from frontier technological progress. The toy example assumed that everyone benefits from frontier technological progress. After all, people in all continents use technologies like smart phones, cars and solar panels.

However, I’m very uncertain about whether people in low-income countries will ever feel the full benefits of frontier TFP growth. For example, some agricultural R&D done in the US won’t ever be applicable in countries with different climates. Currently, I assume (arbitrarily) that if frontier TFP increases by 10% then TFP around the world will eventually increase by 7%.^[14]The lag until productivity benefits are felt will probably be larger in low income countries than in high income countries. As mentioned above, I don’t model this lag because it wouldn’t affect the results by much. I use a discount of 0.2%, so a 50 year lag would reduce the returns to R&D … Continue reading This part of the calculation is particularly uncertain about and I’m interested in suggestions for how to think about this. This adjustment multiplies the social returns to R&D by a factor of 0.7.

I only give R&D partial credit for productivity growth. Activities with a potential claim to credit include misallocation reduction, business innovation (e.g. startups), learning by doing and capital accumulation. Ultimately, I credit R&D with 40% of productivity growth and explain my reasoning here. This straightforwardly multiplies the bottomline by 0.4. In an appendix, I briefly sense-check this assumption against studies using statistical techniques to tease out the causal impact of R&D on growth. Naively, this suggests I should give R&D more credit for growth, but there are a number of complications involved in the comparison.

I assume diminishing returns to adding more researchers within any given year. The toy example assumed that if you increase R&D funding by 1%, you’ll make 1% more R&D progress. That logic implies that doubling R&D funding would double the rate of R&D progress. However, there may in fact be diminishing returns to spending, e.g. because some research effort is duplicated. In line with this, the model assumes that the marginal $ spent on R&D causes only 75% as much R&D progress as the average $ spent.^[15]In economic growth models, this corresponds to the “stepping on toes” parameter λ = 0.75. I’m not aware of data that pins down λ, and it seems like values between 0.4 and 1 could be correct. I use the estimate from Bloom et al. (2020) Appendix Table A1, where they set λ = 0.75 and then … Continue reading

I incorporate capital deepening: higher productivity → more machines → higher incomes. Suppose you invent a drug (e.g. caffeine) that makes everyone slightly better at their jobs. We can distinguish between two effects. A primary effect is that everything people buy is higher quality – e.g. better haircuts, tastier food, faster transport – because the people producing these goods and services are better at their jobs. A secondary effect is that when people and companies invest in buying tools to help them do their jobs (e.g. computers), they’ll get more tools. After all, the people producing these tools are better at their jobs. Having more tools makes people better at their jobs. In the economics literature, this secondary effect is called capital deepening.^[16]The primary effect is recorded as a TFP increase because GDP went up holding constant the amount of labour and physical machinery. The secondary effect is recorded as capital deepening because each person has more physical capital (i.e. more or better machinery).

Both effects ultimately increase the quality or quantity of goods and services produced, and so raise incomes. My toy example included the primary effect, but not the secondary effect. Including both effects increases the benefit by a factor of 1.5.^[17]Growth theory relates the size of these effects on income: (income increase from TFP and capital deepening) = (income increase from TFP alone) / (1 – capital share of GDP). The capital share is about 35%, so this multiplies the bottom line by 1 / (1 – 0.35) = 1.5.

Bottom line – social returns to R&D

Once we incorporate all these changes to the toy example, what are the social returns to R&D?

The toy example found that a marginal $20 billion to R&D has the same welfare benefit as increasing the incomes of 400 million people by 10% for one year. (In fact it would increase many more people’s incomes by a much smaller amount; the log-utility model allows us to express the welfare benefit in this way.)

With these changes, $20 billion to R&D has the same welfare benefit as increasing the incomes of 180 million people by 10% each for one year. (Again, it would actually increase many more people’s incomes by a much smaller amount; the log-utility assumption allows us to express the welfare benefit in this way.)

This is 45% of the benefit calculated in the toy example. We can break this decrease down into a 0.4 penalty from only giving R&D partial credit for productivity growth, a 0.7 penalty from uncertainty about whether frontier TFP progress really spills over to the whole world, and a 1.5 gain from capital deepening; combining these yields a 0.42 penalty. Then the other changes mostly cancel each other out. (If you want to know more, there’s a full description of the model in this appendix.)

To make this result more relatable, let’s consider smaller expenditures. Dividing both the costs and benefits by 180 million, ~$110 on R&D has the same welfare benefit as increasing one person’s income by 10% for one year.

These returns are high. However, they’re not as high as cash transfers to people in global poverty. $110 to someone living on $500/year increases their income by 22% for one year.

Intervention	Welfare impact of $20 billion	Welfare impact of $110	Cost effectiveness in Open Philanthropy’s units of impact
R&D (final calc)	Increase the incomes of 180 million people by 10% for 1 year.	Increase the income of one person by 10% for 1 year.	45X
R&D (final calc)	In fact, R&D would increase many more people’s incomes by a much smaller amount and for a much longer time; the log-utility model allows us to state the benefit in this way.		45X
Cash transfers to people on $500/year^[18]As mentioned in a previous footnote, I think GiveDirectly is somewhat more impactful than the numbers in this row.	Increase the incomes of 400 million people by 10% for 1 year.	Increase the income of one person by 22% for 1 year.	100X
Cash transfers to people on $50,000/year	Increase the incomes of 4 million people by 10% for 1 year.	Increase the income of one person by 0.22% for 1 year.	1X

The GHW team at Open Philanthropy aims to only make grants whose expected impact is above a certain bar. Our current tentative bar is 1000X, as measured in units where “1X” is giving $1 to someone earning $50k/year. In these units R&D comes out as 45X, 4.5% of the bar.

There’s an important sense in which this comparison is biased in R&D’s favour. The calculated benefits from R&D include those that occur many decades into the future, while the income increase from a cash transfer is immediate. If we included long-run benefits from cash transfers, they would beat R&D by a wider margin.

The best pro-growth interventions are better than average R&D

One important caveat is that there may be leveraged ways to boost the amount of R&D. For example, lobbying for more high-skilled visas could increase the effective global number of skilled R&D workers, accelerating R&D progress more than paying for R&D directly.

A second caveat is that we’ve estimated the average impact of marginal R&D funding. Of course, the actual impact of any particular grant could be much larger or much smaller than this, depending on the project being funded. If a funder can consistently identify particularly promising projects, their impact could be larger than my estimate. One way to do this might be to focus on R&D projects that are specifically designed to help the global poor. Just as $1 goes further when transferred to the global poor, so too R&D might be more effective when targeted in this way.

Some of those involved with Progress Studies think accelerating innovation should be the world’s top priority. I discuss ways in which my outlook differs from theirs in this appendix.

Funding R&D was even better in the past

Today the returns to R&D are high. I think that they were even higher in the past for a couple of reasons.

R&D was more neglected. We’ve seen that ideas are getting harder to find over time as the easiest ones are discovered. In the past, much less R&D had been done in total and so ideas were significantly easier to find. Appendix F estimates that the fraction of the economy dedicated to research was 36 – 96X smaller in 1800 than today.

R&D increased the amount of R&D occurring at later times. I think that, historically, there were two mechanisms by which R&D caused more R&D to occur at later times.

Increasing the fraction of resources used for R&D. The first is providing evidence that R&D was a worthwhile activity. The fraction of people doing R&D has increased significantly over time.^[19]For example data from Bloom et al. 2020 find the number of US researchers increasing by 4.3% per year on average since 1930. US population grew less than 1.5% per year on average in the same period, implying that the fraction of people doing research was growing.
Earlier instances of R&D are probably an important reason, as their success fuelled the expansion of R&D efforts. The mechanism is: R&D → evidence of success → more R&D. Today this mechanism is probably less important, as there is already ample evidence of the fruitfulness of R&D (though funding specific neglected areas of R&D can have a similar effect today if you are better at predicting fruitful areas than the average funder).
Increasing the future population. The second is that, going back hundreds and thousands of years, productivity improvements allowed a fixed supply of land to support larger populations, which meant more people to engage in innovative activity (though the fraction of people doing so was very low). The mechanism is: R&D → fixed supply of land can support larger populations → more people are alive to do R&D in the future. This dynamic is important in some prominent models of long-run growth.^[20]See for example Lee (1988), Kremer (1993), Jones (2001) and Galor and Weil (2000). Today this mechanism is not important: population growth is determined by people’s fertility decisions rather than by how many people society is able to feed.

A back-of-the-envelope calculation suggests that the combined effects of these mechanisms could be very large, with the social impact of R&D hundreds of times greater in the past than today.

So it may be that historically R&D was the most promising philanthropic intervention, even if it isn’t quite as promising today.

Limitations of the model

The model ignores potential harms from R&D

Certain types of R&D might have large downside risks. For example, gain of function research can make pathogens more deadly and transmissible, potentially increasing global catastrophic risk from a pandemic.

This consideration might make funding certain types of R&D very harmful, reversing the conclusion of the model. I think it would be a mistake to act on the basis of this post without explicitly considering these downside risks.

Evaluating which types of R&D pose the largest risks is beyond the scope of this post. This is a significant limitation, and highlights that this post gives a stylized estimate of the returns to R&D but does not give an all-things-considered assessment.

The model implies growth will stagnate

My mainline scenario, used for the stylized calculation, implies that productivity growth will tend to 0% per year in the very long run.

Why does this happen? It’s the combination of two assumptions:

Ideas are getting harder to find. Each 1% increase in productivity requires more research effort over time, even accounting for the fact that researchers can use new technologies to aid their research effort.
Population stagnation. Population will rise to 11 billion and then remain roughly constant.

Together these two assumptions imply the pace of productivity growth will slow. Population stagnation implies that the number of researchers will eventually stagnate.^[21]Though the fraction of people doing research can increase, this can only go on for so long. I discuss this possibility below. Ideas are getting harder to find then implies that it will then take increasingly long to find each new idea. This implication is explored in depth in Jones (2020).

The following graph shows my model’s prediction of productivity stagnation alongside a scenario where TFP grows exponentially at its recent historical rate forever.^[22]There are good theoretical reasons to think TFP can’t grow exponentially at its recent rate for more than 10,000 years, but these don’t rule out exponential growth continuing for another 1000 years.

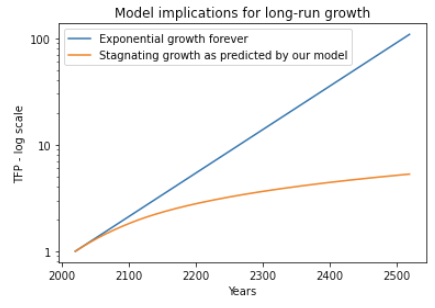
Productivity stagnation is a surprising implication of the model; people might wonder whether the model is overly pessimistic about productivity growth.

To address this, I explored four alternate scenarios in which productivity doesn’t stagnate:

Maybe we’ll avoid productivity stagnation by increasing the fraction of people doing R&D (even more than in my model)?
Maybe ideas will not get harder to find in the future?
Maybe the world’s population won’t stagnate?
Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find? More.

I did very rough back-of-the-envelope calculations of how the social returns to R&D change in each scenario. Scenario 1 reduces the returns to R&D, multiplying the bottom line by ~0.4X. Scenarios 2 – 4 can multiply the bottom line by up to ~7X, or much more for some versions of scenario 4.^[23]If R&D today expedites a future technology that massively accelerates future growth, the bottom line can increase by much more than 100X. More.

If I did a weighted average across these scenarios, it would probably increase my bottom line compared to simply using the mainline scenario. (The size of the increase would be very sensitive to the specific weights used, especially for the versions of scenario 4 with massively outsized returns.)

For now, the stylized estimate at the top of this post doesn’t put any weight on these scenarios. One reason for this is that the stylized estimate excludes scenarios where R&D causes large harm, so it feels fair to similarly exclude trend-breaking scenarios where R&D has large upsides. Another reason is that I want the stylized estimate to be comparable with Open Philanthropy’s impact estimates for other Global Health and Wellbeing cause areas, and we don’t consistently place weight on unlikely scenarios with large upsides.

In addition, I have specific reasons for excluding each of the four scenarios:

My mainline scenario already involves significant increases in the fraction of people doing R&D. More.
This scenario seems very implausible. More.
The high returns in this scenario are driven by tiny benefits enjoyed by a massively expanded population 100s of years into the future. More.
Conditional on the development of such a growth-boosting technology in the next century, Open Philanthropy currently prioritizes work reducing risks from this technology over work accelerating its arrival. More.

That said, I’m very uncertain about how much weight the GHW team should place on these scenarios and I think there is room for reasonable disagreement. It’s worth noting that even a 7X increase would leave unlevered R&D funding ~3X less effective than Open Philanthropy’s bar for funding within GHW (though it would likely imply that various levered advocacy or research spending opportunities should make up much more of our portfolio).^[24]My mainline scenario found R&D to be 45% as impactful as giving cash to someone on $500/year. This implies R&D is 4.5% as impactful as our current bar for GHW grantmaking. A 7X increase would leave R&D 31.5% as impactful as the GHW bar.

I find scenario 4 the most plausible, and discuss it further in the next section. I discuss scenarios 1 – 3 at greater length in this appendix.

Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find?

Increasing research effort has been required to find new ideas, even though previous discoveries have made researchers more productive (e.g. calculators, coding tools, caffeine, the internet). Extrapolating this trend, we’d predict that future technological progress will make researchers somewhat more productive but that this won’t be enough to avoid productivity stagnation.

Perhaps, though, this trend won’t continue. Perhaps future technologies will enhance our research abilities more than those from the last 80 years. For example, if we develop advanced AI systems that can do independent research we might massively increase our research efforts.^[25]Aghion et al. (2017) discuss the possibility that AI will accelerate productivity growth by automating research tasks. Another possibility is advanced bio-technology that radically enhances the productivity of human researchers. Call such technologies growth-enhancing technologies.^[26]Note, a growth-enhancing technology might allow a constant population of human researchers to maintain ~2% productivity growth, or it might allow them to accelerate productivity growth. Open Philanthropy thinks the latter possibility is more likely than many actors seem to think, for reasons … Continue reading

Past technologies have enhanced research productivity somewhat, but we’ve still had to increase the number of human researchers to maintain constant productivity growth. Growth-enhancing technologies would (by definition) allow us to maintain constant productivity growth without increasing the number of human researchers.^[27]Of course, growth-enhancing technologies might enable other trends to continue. E.g. the trend of ~2% annual growth in US GDP/capita over the past 150 years, or the trend of growth accelerating over the past 10,000 years.

If a growth-enhancing technology is developed sometime in the future, how would this alter the value of R&D today?

It turns out that this depends on whether R&D today affects the time at which the growth-enhancing technology is developed.

If R&D today doesn’t affect when a future growth-enhancing technology is developed, then its development reduces the value of R&D today. This is somewhat counter-intuitive: although more total R&D will happen, the marginal value of R&D today is lower. The reason is related to ideas getting harder to find. More R&D in later periods pushes us further up the diminishing returns curve for finding new ideas, so the additional R&D we funded makes less difference.^[28]Let’s demonstrate this point with an example. Suppose an intervention causes an extra researcher-year to happen in 2021. Let’s consider its impact on TFP in 2100 if a growth-enhancing technology isn’t developed, and if it is developed. Suppose that if a growth-enhancing technology isn’t … Continue reading

If R&D today accelerates the development of a future growth-enhancing technology, its impact on future incomes could be much larger than my estimate. It would bring forward in time an income boost, raising people’s incomes for a long time into the future.^[29]Appendix D does a very rough BOTEC on the returns to R&D for one possible growth-enhancing technology.

If this is the scenario anticipated by proponents of a “growth-first” worldview or the Progress Studies community, I think this would be worth being more explicit about; I take them to more typically be arguing from past trends rather than speculating about future trend-breaking technologies.

Open Philanthropy institutionally thinks the possibility of these sorts of trend-breaking future technologies is notably higher than many other actors in society seem to, and the Longtermist team of OP focuses explicitly on optimizing the expected impact of their spending in the world where such technologies are likely in the next century or so. However, conditional on placing high probabilities of the development of such technologies in the next century, the Longtermist side sees work on accelerating growth as lower impact than work reducing risks.^[30]Eg. see this draft report by Joe Carlsmith on risk from power-seeking AI, or these two posts from the Cold Takes blog.

Absent more external consensus, we’re reluctant to have the prioritisation of our Global Health and Wellbeing team be driven by the possibility of trend-breaking future technologies. This is for reasons related to our views on worldview diversification.^[31]Even if R&D isn’t competitive according to either worldview, might it look competitive according to a weighted sum of both? I think not. I estimate funding generic R&D to be ~10X worse than the GHW bar, and it looks significantly worse from a LTist perspective than alternative … Continue reading As such, I am currently not putting significant weight on this scenario in evaluating the social returns to R&D. We’d be interested to know if advocates for the primacy of growth or Progress Studies think that such trend-breaking future technologies are likely and/or crucial to their case for prioritizing growth going forward — that hasn’t been our impression from what we’ve read — and if so how they think about prioritizing growth relative to reducing longterm risks.^[32]Appendix H discusses some potential differences between my perspective and that of Progress Studies advocates.

Other limitations of the model

Appendix K discusses two more debatable assumptions made by the model:

It assumes that increasing the amount of R&D in 2021 doesn’t affect the amount of R&D effort in future years.
It assumes that welfare increases with log(income).

In both cases, the assumptions of the model could be too aggressive or too conservative about the returns to R&D.

Appendix J lists additional ways in which the stylized calculation is arguably pessimistic or optimistic about the social returns to R&D.

How significant are these limitations?

I think these limitations are very significant. Including the downsides to R&D could make the returns to R&D substantially worse or even negative, while putting weight on scenarios with extreme upside could make the returns much better.

Conclusion

The model discussed here gives Open Philanthropy a stylized value for marginal R&D spending that we may use in our GHW cause prioritization work. It suggests that the social returns to direct R&D spending are high, but not as high as some opportunities relating to poverty alleviation. Still, leveraged ways to boost R&D activity could be highly impactful, and Open Philanthropy may enter causes like high-skill immigration or science policy in part because of this modeling.

In addition, the research leaves me relatively skeptical of arguments that accelerating innovation is the primary social priority going forward. I estimated marginal R&D spending to be 4.5% of the GHW bar. Even if we ignore potential harms from R&D and consider an alternative scenario where R&D is 7X more valuable, directly funding R&D still doesn’t meet the GHW bar. The only scenario I considered where R&D returns are higher still – R&D today accelerates the development of a growth-enhancing technology – is one where Open Philanthropy currently, and in my view correctly, prioritizes reducing risks over accelerating timelines.

The stylized estimate in this post has huge limitations. Perhaps most important is that it excludes potential harms from R&D, and accounting for this factor could reverse the conclusion of the model. Based on this, and the model’s many other limitations, I see this post as opening a conversation about the returns to R&D rather than closing it.

Description of the appendices

The appendices, contained in a public google doc, dig into various aspects of this post in more detail. I recommend only reading appendices that are of particular interest.

Appendix A explains the model used in the stylized estimate of the returns to R&D, including all the assumptions needed to recover the result.
Appendix B and appendix C do a deep dive into the model’s implications for how marginal R&D affects incomes in the short run and the long run.
Appendix D contains very rough estimates of the social returns to R&D in the alternative scenarios mentioned in the main post, allowing for a comparison with this post’s mainline scenario. Appendix E discusses some of these alternative scenarios qualitatively. The main takeaways from these two appendices were discussed above.
Appendix F contains a very rough estimate of the returns to R&D in 1800. The key takeaway is that incorporating the qualitative differences discussed above implies that R&D in 1800 could have been more than 100X more impactful than R&D today.
Appendix G sanity checks some of the assumptions of the model used in this post against economics papers that use statistical techniques to try and tease out the causal effect of R&D on growth.
Appendix H discusses how my current view differs from the views of those involved in the Progress Studies movement.
Appendix J lists ways in which the stylized calculation is arguably too optimistic or too pessimistic about R&D spending.
Appendix K briefly explores alternatives to two assumptions of the stylized calculation. The assumptions are:
- The model assumes that increasing the amount of R&D in 2021 doesn’t affect the amount of R&D effort in future years; but it might increase or decrease it.
- The model assumes that welfare increases with log(income).

Note that the calculations in the appendices are somewhat less vetted than those in the main text. The main text calculations have been reproduced using multiple methods, and checked by other researchers at Open Philanthropy.

Appendix A: Assumptions of the model

The calculation proceeds in two stages. First, I run a simple simulation to estimate the social impact of R&D. Second, I make a series of adjustments to make the bottom line more realistic.

Simulation assumptions.
Adjustments made to simulation output.
Full list of assumptions.

Simulation assumptions

What model of R&D am I using?

I use the semi-endogenous growth model of Jones (1995).

TFP growth is given by:

$ g_A = constant * L^{\lambda}A^{\phi – 1} $

$ L $ is the number of researchers, A is the level of TFP, $ g_A $ is the growth rate of TFP.

$ {\phi} $ and $ {\lambda} $ are constants that control the diminishing marginal returns (DMR) to R&D. The lower these constants, the steeper the DMR.

$ \lambda $ controls the DMR to more researchers at a given point in time (“stepping on toes”)
- If $ \lambda $=1, doubling researchers in a year doubles the TFP growth in that year
- If $ \lambda $=0, doubling researchers in a year doesn’t change TFP growth that year.
- If $ \lambda $=0.4, doubling researchers in a year increases TFP growth by 1.3X.
- I think 0.4<<1 is reasonable.
  - Unfortunately, this is based on little but intuition. I think <1 because I think there are a few plausible mechanisms for giving at least a small stepping on toes effect. I tentatively think >0.4 because I’d be surprised if doubling the number of researchers speeds up R&D progress by <1.3X. I’m very interested to hear about further evidence on this point.
$ \phi $ controls whether progress today makes future progress harder
- The smaller $ \phi $, the more progress today makes future progress harder (“fishing out”).

What can the empirical data tell us about $ \phi $ and $ \lambda $?

The basic empirical trend is that (# researchers) has grown exponentially over the past 80 years, but TFP growth has stayed roughly constant.

Let’s assume that the R&D effort has been driving the TFP growth (or some constant fraction of it). Then there are then two explanations you could give for why TFP growth has stayed constant:

Adding more researchers in a given year doesn’t actually increase the progress made very much. There’s a big “stepping on toes” effect. Small $ \lambda $.
Each 1% increment in TFP is harder to achieve than the last. So more progress is required to achieve it. There’s a big “fishing out” effect. Small $ \phi $.

We can have (1) and (2) in various different combinations, as long as their combined effect is strong enough to explain the basic empirical fact. If you increase $ \lambda $, you’ll need to decrease $ \phi $ to compensate and make your predictions consistent with the historical data.

So the historical data don’t pin down both $ \phi $ and $ \lambda $ separately. Instead, I make an assumption about $\lambda $ and the data pins down $ \phi $. Two options mentioned in Bloom et al. (2020) are:

$ \lambda $=1, $ \phi $=-2.1
$ \lambda=0.75 $, $ \phi $=-1.4

I use the second; serial bottlenecks do place DMR on parallel research and marginal researchers are less talented (if our intervention increases researcher-concentration).

In appendix B I explain the consequences of this model for the social returns to R&D. The rest of this appendix continues to list the assumptions used.

How do I apply this model in the simulation?

The simulation compares utility in two worlds. In world 1 we slightly boost the amount of global R&D activity for 1 year.^[33]The simulation assumes that the increase in R&D activity is proportional to the increase in funding. This may be optimistic: in reality you need both funding and researchers to do R&D. Essentially, the simulation assumes that more funding will bring with it more researchers, which may be … Continue reading In world 2 we do nothing. After this first year the R&D activity is the same in both worlds.

The simulation applies the R&D equation above in each year; making assumptions about the number of researchers L in each year and calculating the resultant TFP trajectory. It assumes R&D instantaneously boosts TFP around the whole world. It assumes incomes are proportional to TFP,^[34]So it ignores the additional effect that capital deepening has on TFP increases in standard growth models. and calculates income trajectories for worlds 1 and 2.^[35]It assumes everyone is on the world average income. Representing income inequality wouldn’t change the results. This is because we ultimately care about the percentage effect of R&D on income, and this is the same no matter what people’s starting incomes are. We care about the percentage … Continue reading It then converts these to utility trajectories, assuming utility = k + m*ln(income).^[36]The specific values used for k and m do not affect the result as they cancel. In practice we use k=0 and m=1. It makes assumptions about the world population to calculate the total difference in utility between worlds 1 and 2 in each year.

To quantify the result, the simulation compares the utility from funding R&D to the utility that could have been achieved by increasing the consumption of someone on the average global income.^[37]It quantifies the result in this way because this is a metric Open Philanthropy uses internally to compare the impacts from different kinds of intervention.

In particular, the simulation calculates the following quantity:

$ Impact \, multiplier = (utility \, from \, TFP \, gains \, of \, \$1 \, to \, R \&D) \, / \, (utility \, from \, \$1 \, to \, average \, world \, consumption) $

Other simulation assumptions

The simulation makes assumptions about the world population in each year and about the fraction of the world population who are researchers in each year.

Population
- The current population is 7.9 billion.
- Population increases at 0.4% per year until 2100, when it reaches 11 billion.
- Thereafter the population remains constant at 11 billion.
Fraction of population who are researchers
- This eventually increases by a factor of 13 compared to today.
- The fraction of the population doing research is proportional to ‘research intensity’, the fraction of GWP spent on R&D.
- Current research intensity = 2.3%.
- Research intensity increases linearly at an absolute rate of ~0.05% per year until it reaches 30%.^[38]More precisely, the absolute size of the annual increment is 2% of current research intensity: 0.02 * 2.3% = 0.046%. So this assumption corresponds to thinking that research intensity has been growing exponentially at about 2% per year, but this exponential rate of increase will decline over time.
  - 2050: 3.7%
  - 2100: 6%
  - 2200: 10.6%
  - 2300: 15.2%
  - 2500: 24.4%
  - The research intensity increase can be understood as including the effects of catch-up growth. When countries develop they typically increase their R&D output; for example R&D from India and China is likely to significantly increase this century.

Adjustments made to simulation output

Expressing the benefit in terms of a % income increase

Most readers should skip this section. It describes a conceptual adjustment from the ‘impact multiplier’ metric used in the simulation to the ‘% income increase’ metric used in this blog.

The simulation calculates the following quantity:

$ Impact \, multiplier = (utility \, from \, \$1 \, to \, R \&D) \, / \, (utility \, from \, \$1 \, to \, average \, world \, consumption) $

It finds that this quantity = 21. Rearranging:

$ (utility \, from \, \$1 \, to \, R \&D) = 21 \times (utility \, from \, \$1 \, to \, average \, world \, consumption) $

Average world consumption (in nominal terms) is ~$10,000, so $1 to average world consumption would increase one person’s income by 0.01% for one year.

$ (utility \, from \, \$1 \, to \, R \&D)=21 \times \, (utility \, from \, increasing \, one \, person’s \, income \, by \, 0.01 \% \, for \, one \, year) $

$ (utility \, from \, \$1 \, to \, R \&D)=(utility \, from \, increasing \, 21 \, people’s \, income \, by \, 0.01 \% \, for \, one \, year) $

Multiplying the costs and benefits by 20 billion (in line with the discussion in the main text):
$ (utility \, from \, \$20b \, to \, R \&D)=(utility \, from \, increasing \, 420 \, billion \, people’s \, incomes \, by \, 0.01 \% \, for \, one \, year) $
$ (utility \, from \, \$20b \, to \, R \&D)=(utility \, from \, increasing \, 420 \, million \, people’s \, incomes \, by \, 10 \% \, for \, \, one \, year) $

Substantive adjustments

I multiply the above number by 0.42 due to three adjustments: 0.7 for the possibility that productivity benefits are not felt worldwide, 0.4 because I only credit R&D with 40% of TFP growth, and 1.5 because higher TFP leads to capital deepening. This implies:
$ (utility \, from \, \$20b \, to \, R \&D) = $
$ =(utility \, from \, increasing \, 420 \, million \, people’s \, incomes \, by \, 10% \, for \, one \, year)*0.42 $
$ =(utility \, from \, increasing \, 180 \, million \, people’s \, incomes \, by \, 10% \, for \, one \, year) $

This gets us to the bottom line quoted in the main body. This sheet contains the above calcs for getting from the simulation output to the table in the main body.

The next section explains the 0.4X adjustment in more detail; the others are explained in the main post.

What proportion of productivity benefits should we credit to R&D?

I multiply by a factor of 0.4 because I credit measured R&D with 40% of productivity growth. Deciding how much credit to assign to different sources of income growth is a major source of uncertainty, and I don’t know of a principled and fully satisfactory approach for doing this. My reasoning was as follows:

Misallocation reduction gets 25% of the credit. This is based on Hsieh et al. (2013), which estimates that improvements in the allocation of talent explains 24% of growth in GDP/worker. A similar adjustment is made by Jones (2021).
- You could argue this adjustment is unnecessary if other changes, not measured in Hsieh et al. (2013), had an opposing effect. For example, housing constraints, bad institutions for infrastructure, and regulation of tech like nuclear energy might have reduced TFP.
Learning by doing gets 0% of the credit.
Although learning by doing does lead to productivity improvements, this happens downstream of the introduction of new production processes. Without these new production processes, learning by doing would eventually dry up. I give the ultimate credit to the R&D (and other types of innovation) that develops these new production processes in the first place.
- What we really care about is the counter-factual: if R&D progresses faster than it otherwise would have, what effect will this have on productivity growth? In this context, I am claiming that if R&D progressed faster, learning by doing would speed up in response (with a lag). The extra R&D would be counterfactually responsible for both more R&D progress and more learning by doing.
Measured R&D gets 55% of the remaining credit for innovation.
- In Eurostat’s survey of 28 countries, firms reported that R&D is 55% of total innovation costs.^[39] See page 20 of Jones and Summers (2020). The other costs are linked to acquiring new equipment and software.
- You could argue this is overly generous to measured R&D if R&D is systematically under-reported and this won’t be captured by survey responses. Some examples:
  - Wal-Mart sometimes doesn’t report R&D expenses but its logistics innovation has probably contributed to US TFP growth.
  - Innovation related to improving services and introducing more product variety may also not be reported as R&D.
  - Startups are often focussed around highly innovative activities like taking new products to market, but may not bill much of this as R&D.

So I give R&D credit for 0.75*0.55 = ~40% of TFP growth.

Another method for arriving at ~40% is to assume that the combination of R&D spending and all net investment is responsible for 100% of growth. Applying this within the US, R&D spending is 2.7% GDP and net domestic investment is 4% of GDP. so the R&D spending is responsible for 2.7/6.7 = 40% of TFP growth.

In an appendix, I sense-check this assumption against studies using statistical techniques to tease out the causal impact of R&D on growth. Naively, this suggests I should give R&D more credit for growth, but there are a number of complications involved in the comparison.

Full list of assumptions

Utility = k + m * log(income)
R&D equation:
- $ g_A = constant * L^{\lambda}A^{\phi – 1} $
  - Or equivalently, $ dA = constant * L^{\lambda}A^{\phi} $
- $ \lambda $=0.75
- $ \phi $=-1.4

L proportional to $ spent

Initial value of $ A $ set by assuming a steady state with $ L $ growing at 3% per year – its average growth over the last 20 years in the Bloom et al. (2020) data set.
- The formula for the steady state value of A is from the equation just below equation (19) on p.53 of Jones and Summers (2020).
- If this initial value was lower, marginal R&D today would be more impactful.
Population
- Current population is 7.9 billion.
- Population increases at 0.4% per year until 2100, when it reaches 11 billion.
- Thereafter the population remains constant at 11 billion.
Fraction of population who are researchers
- The fraction of the population doing research is proportional to ‘research intensity’, the fraction of GWP spent on R&D.
- Current research intensity = 2.3%.
- Research intensity increases linearly at an absolute rate of ~0.05% per year until it reaches 30%. Then it remains at 30%.
- That’s a factor of 30/2.3 = 13 increase compared to today.

Discount rate on future utility: 0.2%
Adjustment for R&D benefits spreading all over the world: 0.7
Proportion of TFP growth credited to R&D: 0.5
TFP gains from R&D increase everyone’s incomes by the same % amount.

You can see the full simulation code here, which provides sources for these assumptions. Alternatively, you can see a spreadsheet version of the calculation here.

Appendix B: understanding the implications of semi-endogenous growth for the social returns to R&D

I think about the impact of the intervention in terms of a ‘TFP wedge’: the % difference in TFP between the worlds with and without the intervention. First, I’ll discuss the initial size of the wedge; then how the wedge changes over time.

(In this section I quote various technical results; I derive these in appendix C.)

What’s the initial size of TFP wedge?

Suppose TFP growth in the world without the intervention is $ g_0 $, and the intervention increases the amount of R&D that year from L to L(1 + v). Then it turns out that the initial size of the wedge is:
$ wedge = {\lambda} g_0v $
$ wedge = {\lambda}* (growth \, without \, intervention)*(fractional \, increase \, in \, R \&D) $
For example, suppose $ {\lambda} $ = 0.5, TFP growth would be 2% without our intervention, and we boost total R&D spend one year by 1%. Then our intervention increases TFP by 0.5 * 2% * 1% = 0.01%.

How does the TFP wedge change over time?

Suppose the initial wedge is x% of total TFP. Over time x% falls towards 0%.

Why? Because ideas are getting harder to find. Suppose we counterfactually insert 1 extra researcher-year in 1800. Every year y after this, rather than R(y) researcher-years having occurred R(y)+1 have occured.

Initially, the level of technology might have been quite low, and this extra researcher-year might make a noticeable difference to TFP. Ideas are still easy to find.

Once the level of technology is high, however, this extra researcher-year makes little difference to TFP. Ideas are now very difficult to find.

To summarize: higher level of technology → ideas are harder to find → the extra researcher-year makes a smaller counterfactual difference to TFP → TFP wedge is smaller. Indeed, it turns out that the size of the wedge is inversely proportional to the level of technology (to some power).

The following diagram shows the technology level for two paths. The orange path is the one without an intervention; the number of researchers grows exponentially. The blue path has the same number of researchers each year as the orange path, except for the first year when it has 3X as many. You can see that the initial ‘ TFP wedge’ between the paths declines over time.

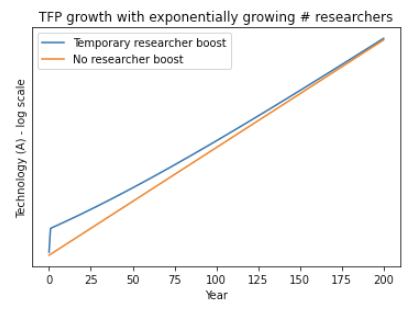
This means that the faster technology progresses, the faster the wedge declines. Faster tech progress → ideas become harder to find more quickly → TFP wedge declines more quickly.

It turns out that the wedge declines at an exponential rate of $ (1-{\phi})g_A $, where $ g_A $ is the growth rate of TFP. In an equilibrium where population grows at a constant exponential rate n, the wedge declines at an exponential rate of $ {\lambda} $n.

This has some interesting consequences.

If population growth is higher, the TFP wedge declines more quickly.
- Faster population growth → faster tech progress → wedge declines faster
- Naively, population growth would dramatically increase the returns to TFP boosts, but this is partly cancelled out by the faster-falling wedge.
- Conversely: a stagnating population would naively significantly lower the returns to TFP boosts, but this is again partly cancelled by the slower-falling wedge. When population is constant, technological progress becomes slower and slower over time (ideas getting harder to find). So the wedge falls more and more slowly over time. If it takes 100 years to halve in size, it will take a further 200 years to halve again, and then 400 years, etc.
If $ \lambda $ is smaller (more “stepping on toes”), the wedge declines more slowly.
- Smaller $ \lambda $ → slower tech progress → wedge declines more slowly

We saw above that smaller $ \lambda $ leads to a small initial wedge. This effect is partly cancelled by the slower decline of the wedge. The “smaller initial wedge” effect dominates, except for very small discounts (<0.3%)^[40]How long does it take for the “wedge declines more slowly” effect to dominate if we have no discount? Let’s assume we change our value of $ \phi $ to compensate when we change lambda. How long does it take for the total impact from $ \lambda $=0.75 to exceed the impact from \( \lambda … Continue reading

Appendix C: deriving quantitative implications of semi-endogenous models for returns to R&D

This appendix derives some results discussed in appendix B and has some further discussion.

What’s the initial size of wedge?

TFP growth is given by:
$ g_A = constant * L^{\lambda}A^{\phi – 1} $

The initial size of this TFP ‘wedge’ is given by:^[41]I get this expression by differentiating the expression for $ g_A $ with respect to $ L $: $ wedge = d(g_A)/dL $.
$ wedge_i = (constant * {\lambda}) / (A^{1- \phi}L^{1- \lambda}) $

What this means is:

The higher the current level of tech $ A $, the smaller the initial impact
The lower $ {\phi} $ (more “fishing out”), the smaller the initial impact
The larger the current research effort $ L $, the smaller the initial impact
- Unless $ {\lambda} $ =1, in which case $ L $ makes no difference
The smaller $ {\lambda} $ (more “stepping on toes”), the smaller the initial impact

If TFP growth in the world without the intervention is $ g_0 $, and the intervention increases the amount of R&D that year from L to L(1 + v), we can simplify the above expression. The initial size of the wedge is:
$ wedge_i = {\lambda}g_0v $
$ wedge_i = {\lambda} * (growth \, without \, intervention) * (fractional \, increase \, in \, R \&D) $

How does the wedge change over time?

The wedge declines over time as the level of technology increases:
$ wedge(t) = wedge_i *[A_i /(t)]^{1- \phi} $
where $ wedge(t) $ gives the size of the wedge at time t, $ A(t) $ gives the level of technology at time t, and $ A_i $ gives the initial level of technology.

Therefore the wedge declines in size at the same rate at which $ A(t)^{1- \phi} $ grows. In other words, at an exponential rate of $ (1- \phi)g_A $, where $ g_A $ is the growth rate of TFP.

If the exponential growth of researchers n is constant, it turns out that the growth rate of $ A(t)^{1- \phi} $ equals $ \lambda n $. This makes sense. The more “stepping on toes” (small $ \lambda $), and the slower researcher growth (small $ n $), the slower the growth of technology.

So the wedge declines in size at an exponential rate of $ \lambda n $.

This can have counterintuitive consequences for how $ \lambda $ affects the intervention’s impact. The more “stepping on toes” (small $ \lambda $ ), the slower the wedge declines over time. In some circumstances, can mean that reducing $ \lambda $ actually increases the impact of the intervention over the very long run, despite the initial size of the wedge being smaller. The intuition is that tech progress is slower at later times, and this means that the intervention’s initial impact diminishes more slowly.

How does the annual utility from the intervention change over time? It decays at the exponential rate
$ (time \, discount) + (decline \, of \, wedge) – (population \, growth) = r + {\lambda}n – n. $
If this quantity is negative (if r is very small and $ \lambda<1 $), the annual utility can grow over time. What’s going on here is the effect of the growing population outweighs that of the declining wedge.

Appendix D: very rough estimates of the social returns to R&D under different scenarios

These are very rough back-of-the-envelope calculations (BOTECs) of the social returns to R&D for a few different scenarios discussed in the blog. I haven’t made a special effort to make these easy to understand, but am including them for completeness.

The first scenario, the ‘mainline scenario’, is a simplified version of the model discussed in the main body of the blog. The others are variants on this model which avoid predicting productivity stagnation.

I calculated how much each scenario changes the returns to R&D compared to the mainline scenario.

	Impact compared to mainline scenario
Scenario	Ignore impacts after 100 years	Ignore impacts after 500 years
Mainline scenario: Ideas getting harder to find and stagnating population drive productivity stagnation.	1X	1X
Maybe we’ll avoid productivity stagnation by increasing the fraction of people doing R&D?	0.7X	0.4X
Maybe ideas won’t get harder to find in the future?	2.3X, or less	6.6X, or less
Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find?	~2X, or much more	~6X, or much more
Maybe the world’s population won’t stagnate?	2.3X, or less	6.6X, or less

The sections below estimate the ‘impact multiplier’, defined as follows:

$ Impact \, multiplier = (utility \, from \, \$1 \, to \, R \&D) / (utility \, from \, \$1 \, to \, average \, consumption) $

This table summarises the results, and was used to construct the above table.

Scenario	Impact multiplier (ignore impacts after 100 years)	Impact multiplier (ignore impacts after 500 years)
Mainline scenario: Ideas getting harder to find and stagnating population drive productivity stagnation.	22X	38X
Maybe we’ll avoid productivity stagnation by increasing the fraction of people doing R&D?	15X	15X
Maybe ideas won’t get harder to find in the future?	50X, or less	250X, or less
Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find?	50X, or less	250X, or less
Maybe the world’s population won’t stagnate?	50X	250X

Mainline scenario: Ideas getting harder to find and stagnating population drive productivity stagnation.

R&D is 2% of US GDP, and currently produces 1% growth in incomes per year.
So 1% extra of GDP on R&D buys an initial income wedge of 0.5%.
This wedge falls over time, as ideas get harder to find.^[42]Why would this happen? We caused some extra counterfactual science to happen: R(t)+1 researcher-years rather than R(t) at each time t. But this extra science makes less % difference to income as ideas become harder to find. 100 vs 101 researcher-years makes a bigger % difference to income than 1000 … Continue reading More specifically, (it turns out that plausible parameters imply that^[43]The wedge halves each time researcher population doubles (assuming the ‘stepping on toes’ parameter $ \lambda $=1). The relationship between TFP growth g and population growth n in steady state is given by g = $ \lambda $ * n / (1 – phi). Using $ \lambda $=1 and $ \phi $=-2 … Continue reading) each time the economy grows by 30% the wedge ~halves.
- (I’m assuming that the amount of R&D in subsequent years is unchanged by our intervention.)
So the wedge first halves after 15 years.
Population is constant but ideas are getting harder to find, so growth slows. More specifically, let’s assume each 30% of growth takes twice as long as the last. As a result, the wedge only halves a second time after 30 years, a third time after 60 years, and a fourth after 120 years.
So the effects of an extra 1% on GDP are roughly as follows:
- 0.5% wedge for 15 years
- 0.25% wedge for 30 years
- 0.125% wedge for 60 years
The total effect in the first 100 years is: 0.5*15+0.25*30+0.125*55 = 22% income boost.
22X direct consumption.
The total effect in the first 500 years is: 0.5*15+0.25*30+0.125*60 + (1/16)*120 + (1/32)*240 + (1/64)*35 = 38% income boost, 38X

Note: this is only a rough BOTEC and gives slightly different results to the full model discussed in the blog. The full model includes a pure discount rate and is more complicated in a number of other ways discussed in the main text post and appendix A.

Maybe we’ll avoid productivity stagnation by increasing the fraction of people doing R&D?

In a sentence “Yes in the last 80 years we’ve needed a growing population to sustain constant growth; but in the future increased R&D intensity will allow us to sustain constant growth with a constant population.”

A rough BOTEC:

R&D is 2% of US GDP, and currently produces 1% growth per year.
So 1% extra of GDP on R&D buys an initial income wedge of 0.5%.
This wedge falls over time, as ideas get harder to find. As above, it halves each time technology increases 30%.
- (I’m assuming that the amount of R&D in subsequent years is unchanged by our intervention.)
So the wedge halves every 15 years.
So the effects of an extra 1% on GDP are roughly as follows:
- 0.5% wedge for 15 years
- 0.25% wedge for 15 years
- 0.125% wedge for 15 years…
So the total effect in the first 100 years is: ~0.5*15*2 = ~15% income boost.
So spending on R&D is 15X direct consumption, with a 100-year horizon.
With a 500-year horizon, the effect is still ~15% income boost, 15X

The returns to extra R&D today are lower than in my baseline stagnation scenario. The extra R&D effort here improves technology faster, making ideas harder to find, so the extra counterfactual science we caused makes less difference.

Maybe ideas won’t get harder to find in the future?

Maybe the observed pattern over the last 80 years will stop, and constant researcher effort will be capable of sustaining a constant rate of rate.

R&D is 2% of US GDP, and currently produces 1% growth per year.
So 1% extra of GDP on R&D buys an initial income wedge of 0.5%.
This wedge is constant over time. It doesn’t diminish because ideas are not getting harder to find.
- (I’m assuming that the amount of R&D in subsequent years is unchanged by our intervention.)
So the total effect in the first 100 years is: 0.5*100 = 50% income boost.
So spending on R&D is 50X direct consumption, with a 100-year horizon.
With a 500-year horizon, the effect is 0.5*500 = 250% income boost, 250X

This BOTEC assumes ideas stop getting harder to find just before our intervention. If they continue to get harder to find for a while, this would reduce the bottom line.

Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find?

For concreteness, suppose R&D today brings forward in time the tech level after which we can sustain 1% annual productivity growth with a constant population. If we bring forward that day by 1 year, we boost income in every year thereafter by 1%.

Rough BOTEC (this one is fiddly):

R&D is 2% of US GDP, and currently produces 1% growth per year.
Currently we need to increase the # researchers each year to sustain exponential growth, but once we reach tech level X a constant # researchers can sustain 1% exponential growth.
1% extra of GDP moves the tech level forward by 0.5 years, and we reach tech level X 0.5 years earlier. Income at all later times is boosted by 0.5%.
Suppose we reach X immediately. Then the total effect in the first 100 years is: 0.5*100 = 50% income boost. That’s 50X.
- The total effect in the first 500 years would be 0.5*500 = 250% income boost, 250X
Suppose we only reach X after 50 years. This would reduce the value of the intervention somewhat, for complicated reasons.
- The benefits in the first 50 years are smaller than 0.5% as the 0.5% wedge shrinks over time.
- If annual research effort has grown, we will reach tech level X less than 0.5 years earlier. E.g. if we do twice as much research by the time we reach tech level X, we’ll only reach it 0.25 years earlier, ~halving the impact each year thereafter.

This is an interesting and complicated case.

We could extend it to consider bringing forward periods of much faster growth, which would make the returns to R&D much higher. For example, if we bring forward an economic singularity (where growth is hyperbolic until it output approaches a very high ceiling), we could be bringing forward a time when all biological humans have lives that are unimaginably happy and fulfilled by today’s standard. In addition, if it’s possible for people to exist as simulations on a computer, that could expand the human population by a trillion-fold or much more.^[44]See Bostrom (2003) for a slightly more detailed explanation of this point. If this happened, it would continue what I believe to be the long-run historical trend whereby R&D has had massive welfare returns by bringing a much richer, more populous and happier future forward in time (see appendix F for more about this model of historical R&D).

Maybe the world’s population won’t stagnate?

In a sentence: “yes ideas are getting harder to find, but the population growth will allow us to meet the demands for ever-more research for each 1% output gain”.

A rough BOTEC:

R&D is 2% of US GDP, and currently produces 1% growth per year.
So 1% extra of GDP on R&D buys an initial income wedge of 0.5%.
This wedge falls over time, as ideas get harder to find. As above, it halves each time technology increases 30%.
So the wedge halves every 15 years.
But each time the wedge halves, the number of people alive ~doubles,^[45]This is exactly true in the semi-endogenous framework when the “stepping on toes” parameter lambda=1. If lambda < 1 then the population more than doubles each time the wedge halves. so the total impact of the wedge is constant over time.
So the total effect in the first 100 years is: 0.5*100 = 50% GDP boost.
So spending on R&D is 50X direct consumption, with a 100-year horizon.
With a 500-year horizon, the benefits would be 250X.

This calc assumed that the population doesn’t stagnate at all. In practice, the realistic version of this scenario is one where population stagnates temporarily. If we incorporate a temporary population stagnation into this BOTEC, the estimated returns to R&D would decrease.

Appendix E: reasons growth might not stagnate, and how that would affect the bottom line

Appendix D contains very rough BOTECs calculating the returns to R&D in each of these scenarios.

Maybe we’ll avoid stagnating growth by increasing the fraction of people doing R&D?

As mentioned earlier, the fraction of people doing R&D (research intensity) has increased significantly over time. If it continues to increase, we can have a growing pool of researchers despite a stagnant population.

This mechanism can temporarily sustain steady productivity growth despite population stagnation. It cannot do so indefinitely as the fraction of people doing research cannot exceed 100% (and will likely cap out much earlier). Indeed, when I incorporate this mechanism into the model, the stagnation of productivity growth is only delayed temporarily.

How does an increasing research intensity in the future affect the impact of R&D today? Counterintuitively, it reduces the impact. The reason is related to ideas getting harder to find. More R&D in later periods pushes us further up the diminishing returns curve for finding new ideas, so the additional R&D we funded makes less difference.^[46]Here’s another way to understand this effect. Because ideas are getting harder to find, the number of new ideas found with a marginal researcher-year is roughly proportional to 1 / (total years of research so far). Suppose we fund an extra year of research in 2021. As a result, in 2050 one more … Continue reading

In fact, the mainline estimate of the social return for R&D does assume that research intensity will continue to increase to some extent. If I put weight on a scenario where there are even greater increases in research intensity, I should also put weight on scenarios where there are smaller increases in research intensity. As it is, I’m happy to just use my central estimate in the stylized calculation of this post.

Maybe ideas won’t get harder to find in the future?

There is strong evidence that ideas became harder to find during the 20th century. But perhaps this is a temporary trend, and soon enough the average difficulty of finding a new idea will stay constant over time.

If this happens, a constant population would be able to sustain constant productivity growth. This would significantly raise the estimated value of today’s R&D. As mentioned above, the model implies that the % income increase due to R&D today will decline over time. But if ideas stop getting harder to find, this decline will stop. In other words, extra R&D today could raise people’s incomes by (e.g.) 0.5% forever into the future. Given my low discount rate, this would significantly raise the estimated social returns to R&D.

I don’t find this scenario plausible. The evidence suggests that ideas have been getting consistently harder to find since 1930, and there’s no reason to expect this trend to change.^[47]See Bloom et al (2020) and https://mattsclancy.substack.com/p/innovation-gets-mostly-harder.

Another version of this claim would be that ideas have never been getting harder to find. Instead our R&D institutions have become exponentially worse over time, and this compounding inefficiency explains why an exponentially growing number of researchers has led to merely constant growth.

Concretely, the data implying that it takes 41X as much research effort to find a new idea than in 1930 is interpreted as implying that institutions have become 41X less efficient. The startling implication is that, if only institutions had remained at their 1930s level, productivity growth would be 41X faster today. That would involve TFP growing by ~40% every year! Again, I don’t find this scenario to be very plausible.

Maybe the world’s population won’t stagnate?

The argument for stagnating productivity growth assumes that the global population will level off at 11 billion. But if the world population grew exponentially in the long-run, growth would not stagnate. The number of researchers could continue to grow exponentially, maintaining constant productivity growth despite ideas getting harder to find.

Is this scenario plausible? It is the UN’s high-end projection out to 2300, and there are some reasons it could happen. Many subcultures and countries currently have very high population growth and, in the long-run, cultural and biological evolution will select for these groups. On the other hand, governments may make a concerted effort to avoid sustained population growth if it would have devastating environmental consequences. Overall, it’s hard to know whether this scenario is likely to happen.

How would sustained future population growth affect the value of R&D today?

Overall, it would significantly increase the value of R&D today. There are two effects, which point in opposite directions. The first effect is that there are more future beneficiaries of today’s R&D, with the number growing exponentially. The second effect is complex. There is more R&D at later times and so the counterfactual impact of today’s marginal R&D on TFP falls over time. In particular, if today’s R&D initially raised TFP by x% then over time x falls exponentially. Combining these two effects, marginal R&D causes a % TFP gain which falls off exponentially over time but is enjoyed by an exponentially growing population. Compared to a case with constant population, the first effect dominates and the impact of R&D is significantly higher.

However, a very large future population would raise the impact of many interventions with positive long-run effects. So it’s not clear that this scenario gives us reason to prefer R&D in particular. Partly on this basis, I’m not currently adjusting the stylized estimate based on this scenario.

Appendix F: back-of-the-envelope calculations of value of R&D in 1800

This appendix estimates the value of R&D in 1800 using a method that incorporates the two factors mentioned in the main text:

Historically, R&D was more neglected than it is today.
Historically, R&D increased the amount of R&D occurring at later times, both by increasing the fraction of resources used for R&D and by increasing future populations.

The calculation is very rough. Its purpose is to highlight just how much these two factors can increase the importance of historical R&D; it shouldn’t be interpreted as a precise estimate of R&D returns in 1800. The choice of 1800, rather than another year, is largely arbitrary.

The calculation uses a different model to one described in the main text to incorporate the second factor: R&D increasing the amount of R&D occurring at later times. The model implies that a researcher-year in 1800 was hundreds of times more impactful than in 2020.

Explaining the model

Suppose (as a toy example) that in 1800 there were exactly 100 researchers. What is the impact of funding an extra researcher-year in 1800? The assumption of this model is that the impact is to bring forward the technological level of the present world by 1/100 years. In other words, we start enjoying the level of wealth of the modern world 1/100 years earlier than we otherwise would have.

Why make this assumption? An extra researcher-year in 1800 means we make more technological progress in 1800. How much more? It increases the number of researchers by 1%, so by the end of 1800 technology is 1/100 years ahead of where it would have been.^[48]101 researchers working for 1 year make the same amount of progress as 100 researchers working for (1 + 1/100) years. Based on the second factor (‘R&D increased the amount of R&D at later times’), this brings all subsequent R&D efforts forward in time by 1/100 years. I.e. the population passes each milestone 1/100 years earlier, and research concentration ramps up on a schedule that’s brought forward in time by 1/100 years. As a result, the whole future trajectory of R&D progress is brought forward by 1/100 years, and we reach modern levels of technology and wealth 1/100 years earlier.^[49]Another way to think about this is that we assume that the total R&D effort at each time is determined by the level of technology. I.e. the level of technology determines both the population and the research concentration and so determines the total R&D effort. So if we reach a given level … Continue reading

So the effect of the extra researcher in 1800 is that we spend 1/100 years less time at 1800 levels of wealth and 1/100 years more time at modern levels of wealth.

How should we value reaching modern levels of wealth x years earlier (and spending x years fewer at 1800 levels of wealth)? The population in 1800 was 1 billion. So a conservative valuation is just the value of raising 1 billion people’s incomes from the average income in 1800 to the average income in 2020. Average global income today is $9600, compared with an estimate of $700 for 1800.^[50] See data from Roodman (2020).

Assuming the log-utility model, this benefit is equivalent to increasing 27 billion people’s income by 10% for x years.^[51]You need ~27 10% income increases to go from $700 to $9600. So you need 27 billion 10% income increases to raise 1 billion people’s income from $700 to $9600. Here I use the fact that all 10% income increases are valued equally, which comes from the log-utility model.
1.1^23 = 14 = 9600 / 700.

A less conservative valuation would also value the additional 7 billion people alive today, or take into account future increases in wealth that we will also reach x years earlier in time.

Applying the model

Currently we spend 2.3% of GWP on R&D.

Let’s say that percentage was 20-30X lower in 1800 — we suggest this is a conservative estimate below. Then R&D was only 0.1% of GWP. How many researchers would that buy? Let’s assume that with 0.1% of GWP you could pay for 0.1% of people to be researchers.^[52]The assumption that researchers earn the average global wage, rather than a higher wage, will make no difference to the result. This is because I will make an equivalent assumption about the wages of researchers in 2020. The results would change somewhat if you think researchers today demand more … Continue reading The world population was 1 billion, so that would pay for 1 million researchers.

Funding an additional researcher-year in 1800 would bring forward the technological level of the present world by (1 / 1 million) years. This benefit is equivalent to increasing 27 billion people’s income by 10% for (1 / 1 million) years; or to increasing 27,000 people’s income by 10% for 1 year.

We can adjust this downwards based on some of the factors considered in the calculation of the value of R&D today:

Stepping on toes. Twice as many researchers make less than twice as much progress due to duplication. 0.75X
Proportion of tech progress credited to R&D. Only 50% of TFP growth comes from targeted R&D. 0.5X
Skepticism about global spillovers of R&D. 0.7X

This reduces the benefit to increasing 7100 people’s income by 10% for 1 year.

How does this compare to the benefit of funding a researcher-year today? The model described in the main body of this implies that the benefit is equivalent to raising 70 people’s income by 10% for a year.^[53]For consistency with the 1800 calculation (see most recent fn), I assume that 1 researcher-year costs the same as the global average income. Today that is about $10,000. The model for R&D today implies that $100 to R&D has the same welfare effect as raising someone’s income by 7% for one … Continue reading

This calculation implies that R&D today has lower returns by a factor of 7100/70 = ~101.

One reason for this large factor is that the calculation in this section assumes an additional feedback loop between R&D and future R&D. I think that this captures a real difference between funding R&D now and in the past; but someone skeptical of that distinction might prefer a smaller factor.

On the other hand, the factor would be much larger if we made any of the following changes:

Used a time before 1800, when the fraction of resources used for R&D would be lower still.
Used a less conservative estimate of the value of arriving at the modern levels of wealth x years earlier (e.g. by placing value on the associated population increase, or by including the benefit of arriving at future levels of wealth x years earlier).
Compare the impact of $1 on R&D today vs in 1800, rather than comparing the impact of a researcher-year. $1 would buy much more research in 1800 than today, as salaries were much lower in 1800.

In light of this, my opinion is that historical R&D was more impactful than R&D today by even more than the factor of 101X estimated above.

We should be cautious with this comparison. As mentioned above, its purpose is to highlight just how much these two factors can increase the importance of historical R&D; it is not a precise estimate of R&D returns in 1800. However, the comparison does suggest that R&D was historically hundreds of times more impactful than R&D today.

Data on the research concentration in 1800

What was the research concentration (% of GWP was spent on R&D) in 1800? I’m not aware of high-quality data on this question. But various sources suggest that research-concentration in 2020 was probably at least 20-30X higher:

Data from Bloom et al. 2020 find the number of US researchers increasing by an average of 4.3% per year since 1930. US population grew less than an average of 1.5% per year in the same period, implying that the fraction of people doing research was growing by 2.8%. This implies a 12X increase in research intensity in 1930 – 2020.^[54]1.028^90 = 12.
Bakker (2013) estimates growth in overall R&D using growth of specific types of R&D funding. One such estimate implies a 1.6% annual growth in research intensity between 1767 and 1904, corresponding to a 8X increase between 1800 and 1930.^[55]1.016^130 = 8 Another such estimate implies a 0.8% annual increase between 1823 and 1941, corresponding to a 3X increase between 1800 and 1930.^[56]1.008^130 = 3.
- Combining these estimates with the Bloom et al. data for 1930-2020 implies a total increase in research-concentration of 36X – 96X.
Utility patents records show large increases between 1800 and 2020.
- E.g. utility patent applications grew 300X since 1850. Accounting for a 15X population increase in the same period, that’s a 20X increase in patent application concentration.
- Design patents similarly show a 30X increase in patent-concentration since 1850.
- This is only weakly informative because patents are just proxies whose correlation with growth-enhancing research effort could chance over time.
Shuttleworth and Charnley (2016) claim science publications grew by 100X between 1800 and 1900. With a 1.6X increase in population in the same period, that’s a publication-concentration increase of 60X in that period alone.
- Again, science publications are only a proxy for growth-enhancing research effort.

Based on the above numbers, a conservative estimate of the increase in research concentration from 1800 to 2020 is 20-30X.

Appendix G: top-down vs bottom-up calculations of the returns to R&D

Summary

This post uses a top-down approach to calculate the returns to R&D, using very high level empirical inputs and an assumption about what fraction of TFP growth is due to R&D. Many economics papers use bottom-up approaches, attempting to tease out the causal effect of R&D from micro-level data. We can use bottom-up approaches to sanity check this post’s assumption about the fraction of TFP growth that is due to R&D.

Bottom up approaches calculate a quantity called the social rate of return, and estimates vary widely between 30% and 130%. The social rate of return can also be calculated using inputs to my model; this calculation gives a value of only 13%. Naively, this implies I’m underestimating the returns to R&D. However, it’s possible that bottom-up approaches overestimate the social rate of return, or that the calculation using my inputs is not really comparable with the results from bottom-up approaches. So I only see this as weak evidence that I’m underestimating the returns to R&D.

Top-down vs bottom-up calculations of R&D returns

The methodology in this post, adjusted from Jones and Summers (2020), is a top-down approach to calculating the social returns to R&D. Its key empirical inputs are very high level quantities: frontier TFP growth and total global R&D expenditures. Based on these quantities, and a simple growth model relating them together, it estimates the welfare benefits from TFP growth then credits R&D with some portion of those benefits. A strength of this approach is its conceptual clarity. A weakness is its reliance on a bald assumption about what fraction of TFP growth is due to R&D.

Many economics papers estimate the social returns using bottom-up approaches. These look for correlations between R&D spending and subsequent TFP growth. Some papers focus on specific technologies or firms or industries. Some study entire countries or even groups of countries. A strength of these approaches is they can potentially identify the causal contribution of R&D to growth by applying statistical techniques to micro-level data and controlling for other causes of growth. Unsurprisingly, this causal identification faces many challenges. A weakness of these approaches is that they aren’t well suited to capturing spillovers that occur far away in space and time because these may not be included in the data used. Indeed, the coefficients estimated typically cannot be translated into all-things-considered estimates of the social returns to R&D without substantive further theoretical assumptions about how the benefit changes over time. In addition, spillovers to low-income countries are typically not included in calculations of the social returns in these papers. Appendix B of Jones and Summers (2020) contains a good overview of bottom-up approaches.

Using bottom-up approaches to calibrate the assumptions of the model in this post

Many bottom-up approaches estimate a quantity called the social rate of return,^[57] See Bloom et al. (2013), Coe and Helpman (1995) and references within Jones and Williams (1998) and Jones and Summers (2020). which means “if I invest a marginal $1 in R&D, how much will GDP increase?”. If the social rate of return is 50%, investing $1 in R&D raises GDP by $0.5. Formally, the social rate of return equals $ dY/dR $, where Y is output and R is the cumulative stock of R&D effort.

Jones and Williams (1998) relate empirical estimates of this quantity to the semi-endogenous model used in this post. They show that
$ r’ = {\lambda}{g_A}/s $
where r’ is an empirical estimate of the rate of return, $ \lambda $ is the stepping on toes parameter discussed in Appendix A, $ g_A $ is the growth rate of TFP due to R&D, and s is the fraction of GDP used for R&D.

We can use the model in this post to calculate the RHS of this equation, and compare it to empirical estimates of the LHS.

This post uses:

$ \lambda $=0.75
$ g_A $ = 1% * 0.4 = 0.4%
- ~1% is the average value of TFP growth over the last 40 years in my data set.
- 0.4 is the fraction of TFP growth I’m crediting to R&D.
s = 2.3%

These imply a social rate of return of 13%.^[58]0.75*0.4%/2.3% = 0.13. This is significantly lower than most estimates in the literature. Bottom-up approaches typically find the private rate of return — which only includes benefits to the innovator — is 20-30%. Estimates of the social rate of return are much higher and vary considerably, at 30 – 130%.^[59]E.g. Bloom et al. (2013) estimate a private return of 21% and a social return of 55%. See multiple estimates in table 1 of Jones and Williams (1998) and in Appendix B of Jones and Summers (2020).

There are a few possible interpretations of this result:

1. This post underestimates the social benefits of R&D.

A natural adjustment would be to increase fraction of TFP growth credited to R&D and to increase $\lambda $. Using $ \lambda $ =1 and crediting R&D with all frontier TFP growth would leave the RHS at 43%.

2. The empirical studies overestimate the social benefits of R&D.

If other causes of TFP growth (e.g. capital expenditures) are correlated with measured R&D, these studies may overestimate the causal effect of measured R&D on TFP growth. Another possibility is that these studies focus on sectors in which R&D is particularly lucrative.

3. The LHS and RHS of the equation are not really comparable, for subtle theoretical reasons.

Here’s one such reason.

The model I use in this post assumes that there is no depreciation of the R&D stock. Once ideas are discovered, they are not forgotten. This means that the measured stock of R&D includes all historical R&D inputs without discount.

But some central empirical estimates of the social rate of return to R&D assume that the R&D stock depreciates at a very fast rate. Coe and Helpman (1995) use a depreciation rate of 5%; Bloom et al. (2013) use a rate of 15%. This means that the estimated stock of R&D only includes R&D inputs from recent years.

If instead these empirical estimates had assumed no depreciation of the R&D stock, they would estimate a larger stock of R&D and so a lower social benefit per $ of R&D stock. The estimated social rate of return would fall.^[60]Conversely, if I’d used the depreciation assumptions used in the empirical estimates, I’d have expected the benefit from marginal R&D to diminish much more quickly over time and calculated a lower total return to R&D.

Fall by how much? A rough calculation suggests Bloom et al. (2013)’s estimate of the R&D stock would rise by a factor of 3, and so their estimate of the social rate of return would fall by a factor of 3 from 55% to 18%. Analogously, the estimate of Coe and Helpman (1995) would fall by a factor of 1.5 from 100% to 67%.

So if bottom-up empirical studies used the same “no depreciation” assumption as I use in this post, their estimates of the social rate of return would fall and the tension with my assumptions would reduce.

This depreciation issue is just one reason the LHS and RHS of the above equation are not straightforwardly compatible. I suspect digging into specific analyses in more detail would uncover further reasons why they are not straightforwardly comparable.

Which of these three interpretations is correct? Interpretations (2) and (3) both seem plausible to me; in combination I think they could explain the discrepancy. That said, I place some weight on interpretation (1) and doing this analysis updated me towards thinking that measured R&D accounted for a greater fraction of TFP growth.

This tension could be investigated further. An ambitious project would be to take the data used in these analyses and use them to directly fit the inputs to the semi-endogenous growth model used in this post.^[61]The model here differs from the standard semi-endogenous growth model in two ways. First, the standard semi-endogenous growth model assumes that all TFP growth is due to R&D; this model relaxes this assumption. Second, this model translates income changes to welfare changes using a log-utility … Continue reading

Appendix H: Potential disagreements with Progress Studies

Progress Studies is an intellectual movement that aims to understand and accelerate civilisational progress. Some people involved in Progress Studies believe accelerating civilisational progress, for example by improving institutions for innovation, should be the world’s top priority.

My conclusion here seems to be somewhat in tension with this. My stylized estimate puts direct R&D spending at 45% the impact of cash transfers to the global poor, and 4.5% the impact of the GHW bar.

The apparent disagreement here may be smaller than it appears.

Firstly, the typical $ spent by governments of rich countries probably has many times less social impact than cash transfers to the global poor. This implies, in line with Progress Studies, that R&D spending has an unusually high social impact compared to typical government spending.

Secondly, leveraged ways to boost long-run innovation, like increasing high-skilled immigration or improving institutions, might be much more effective than directly funding R&D. I expect, partly based on unpublished work by Open Philanthropy, that some such opportunities do meet the GHW bar. In other words, I think that some interventions to boost innovation are among the best in the world for improving wellbeing. It’s not obvious to me that Progress Studies enthusiasts should be interpreted as making a stronger claim than this.

That said, I expect that I do have some substantive disagreements with Progress Studies enthusiasts. In particular:

I expect that ideas will continue to become harder to find. Bloom et al. (2020) offers strong evidence that ideas (defined as insights that increase TFP by 1%) have been getting harder to find for 80 years. This means that even a permanent increase in the fraction of GDP used for R&D only temporarily increases the growth rate. This lowers the returns to R&D compared with if you could permanently increase the rate of economic growth, a possibility that Tyler Cowen highlights in his book Stubborn Attachments.

Some people in Progress Studies have suggested that the evidence from Bloom et al. (2020) might be explained by institutions becoming worse over time.^[62]E.g. see Patrick Collison here, 19:57-25:32. While this may be true to some extent, I don’t think it could be true to such a large extent that ideas haven’t been getting harder to find.
I’m less inclined to place weight on trend-breaking scenarios where funding R&D has a very large upside. Stubborn Attachments acknowledges the possibility that any given intervention might only temporarily increase growth, but argues we should do an expected value calculation and put some weight on the possibility that we can permanently increase the economic growth rate. I feel reluctant for GHW grantmaking to place much weight on trend-breaking scenarios where the upside is very large; see here, here and here for further discussion. This is especially compelling when combined with the next point.
I’m more wary of potential harms from R&D. Part of the reason I’m not inclined to put weight on scenarios with very large upside is because I’m not explicitly modeling possible harms. As mentioned above, this is not an all-things-considered analysis, but more like “How good does R&D look if we use our median estimate of R&D returns and future population growth, ignoring scenarios that could massively increase or massively decrease the returns?

Appendix J: ways in which the stylized estimate is too pessimistic vs too optimistic

Some assumptions of the report are listed as both “arguably too optimistic” and “arguably too pessimistic”.

Arguably too optimistic

The stylized calculation:

Ignores potential harms from R&D, which could dominate the benefits in some cases.
Gives R&D substantial credit for long-run growth.
- An alternative view is that credit for growth should be distributed fairly evenly over economic activities rather than heavily concentrated on a few types of activity. For example, if R&D activity stopped tomorrow, growth would continue for decades due to learning by doing, business innovation, and diffusion of existing tech across the economy.
- A core reason I give R&D substantial credit is that over long timescales it seems that these sources of growth would dry up and R&D is necessary to sustain growth.
- On the other hand, many reviewers of this post suggested that I credit R&D with 50% of the TFP growth or more, and this is supported by a naive comparison with bottom up calculations of the returns to R&D.
Assumes significant R&D spillover between countries.
- In my stylized estimate, all global R&D goes into a common pot that boosts incomes around the world.
- In a model in which each country’s R&D was only relevant to their own growth, then the social returns to R&D would vary by country. The R&D in rich countries would be much less impactful than my stylized estimate because it would raise the incomes of fewer people.
- On the other hand, many reviewers of this post suggested that eventually 100% of frontier growth will spillover around the world, rather than the 70% that I assumed.
Uses a utility function that may overestimate the benefits of increasing the incomes of people who are rich relative to those who are poor.
Assumes the marginal $ on R&D is 75% as impactful as the average $. You might think that the smartest people are already doing R&D, and the best projects are already funded, such that the marginal $ is worse than this.
Assumes R&D increases everyone’s incomes by the same %. If R&D increases the incomes of the rich by a larger % than those of the poor, the stylized calculation will overestimate the utility benefits from R&D.
Includes benefits hundreds of years into the future.
- While I think this is right in principle, Open Philanthropy typically only includes near-term benefits in its analyses of philanthropic opportunities. So we should be very cautious when using the social impact estimate here to compare R&D with other opportunities; a naive comparison would give R&D an unfair advantage.
- I use a discount of 0.2%, based on the possibility of a major disruption. Other sources of uncertainty about whether the benefits of R&D will really be felt might argue for a larger discount.

Arguably too pessimistic

The stylized calculation:

Ignores scenarios in which returns to R&D are much higher
- e.g. expediting a large growth increase due to AI
- Taking the expected value over those scenarios would probably significantly increase the estimated expected returns.
Doesn’t give current R&D credit for increasing the amount of research in future years, even though I think this was a significant dynamic historically and accelerating catch-up growth would have this effect.
Assumes ideas are getting harder to find rapidly (i.e. the diminishing returns are steep)
- I use the estimate from Bloom et al. (2020), but my guess is that their data probably overestimate the growth in researchers and so overestimate the steepness of diminishing returns to finding new ideas.
- Also, if innovation institutions have become worse over time (as people in the Progress Studies movement claim), then Bloom et al. (2020) will overestimate the steepness of diminishing returns to finding new ideas.
Assumes that US R&D $ and non-US R&D $ are equally effective in boosting frontier growth, despite US $ being more focussed on frontier growth. An alternative assumption would be that US R&D does more to boost frontier growth per $ than other R&D.
Uses a harsh value for the DMR to R&D. It’s the value from “Are Ideas getting harder to find”, but I think their data probably overestimates the growth in researchers and so overestimates the steepness of returns. Adjusting for this would probably increase the bottom line by 1-1.5X.
Uses a utility function that may underestimate the benefits of technological progress by assuming the only effect is to raise incomes.
Assumes 30% of frontier innovation never spreads around the whole world. This would be fine if I assumed that only the US was driving productivity growth, but it seems kinda harsh when we’re giving all countries’ R&D equal credit for frontier productivity growth.

Appendix K: additional limitations of the model

The model assumes research today doesn’t change the amount of research tomorrow

My model assumes that funding additional research in 2021 doesn’t affect the amount of research effort in future years.

But you might think research today increases the amount of research tomorrow. I claimed this dynamic was important in the past, with successful R&D projects providing evidence that R&D was a fruitful activity. Today, I think this dynamic is especially plausible for small R&D sectors that have the potential to be significantly scaled up. For example, early stage solar panel R&D may have brought forward in time the point at which it was profitable for private entities to invest in R&D. In other words, early solar R&D increased the amount of solar R&D occurring at later times.

Another reason R&D today might increase R&D in later years is if it accelerates catch-up growth. Richer countries spend more on R&D, so faster catch-up growth implies more R&D spending. For example, India and China are contributing an increasing amount to global R&D, and faster catch-up growth would accelerate this process.

Conversely, more research today might remove a promising research project from the pool of possibilities, decreasing the amount of future research. For example, suppose that certain R&D funders only make grants if the project is sufficiently promising. If ideas are getting harder to find, projects will tend to become less promising over time. More research today would accelerate this process, reducing the appeal of future projects and so reducing the amount of future funding.

It seems plausible that R&D today could increase or decrease the amount of R&D that happens in the future. The current estimate doesn’t make an adjustment in either direction.

Uncertainty about the utility function

My calculation assumes that utility increases with the log of income. But there are plausible alternative assumptions that would change the bottom line in both directions.

On the one hand, you might think that utility diminishes more sharply than the log of income. This can be captured by using a CES function of income with $ \eta >1 $. This assumption increases the benefit of extra income for the very poorest people relative to richer people.^[63]I.e. as income falls, the marginal utility of income increases by more.

This favours cash transfers targeted at the world’s poorest people) over R&D whose benefits are spread amongst people at all income levels.

But on the other hand, you might think that the welfare benefits of developing new technologies outstrip the income increases that they cause. For example, between 1990 and 2020 the average US real income increased from $40k to $60k.^[64]https://ourworldindata.org/grapher/gdp-per-capita-worldbank?tab=chart&yScale=log&country=OWID_WRL~USA Imagine someone in 1990 who earns $40k being offered the following choice:

Their income is raised to $60k, and they must spend all their income on 1990 goods and 1990 prices
They receive the average income of someone in 2020, and must spend it on 2020 goods at 2020 prices

Plausibly, the second option is better because of the possibility of using entirely new products like the internet, smartphones, Amazon, etc.^[65]To make the comparison fair, in option 2 you should be forced to buy all goods and services at 2020 prices. This means that some services will be more expensive than in 1990. Even so, I think option 2 is better because there are many new products that are cheap but useful. If this doesn’t seem … Continue reading The implication is that the increase in income underestimates the benefit of technological progress, or (relatedly) that inflation adjustments doesn’t adequately capture the value of new products and services.^[66]How much does the income increase underestimate the welfare benefit of technological progress? You could roughly estimate this by increasing the cash payment in option 1. E.g. suppose you’re indifferent between option 2 and option 1’) A cash payment of $40k. This would imply that the true … Continue reading Using a utility function that adjusted for this would raise the returns to R&D.^[67] Phil Trammell describes one such utility function here. Also see discussion by Matt Clancy in the “What about other benefits?” section of this post.

So some plausible changes to the utility function would reduce the social returns to R&D, while others would increase the returns.

Footnotes[+]Footnotes[−]

Footnotes
1	If environmental constraints require that we reduce our use of various natural resources, productivity growth can allow us to maintain our standards of living while using fewer of these scarce inputs.
2	For example, in Stubborn Attachments Tyler Cowen argues that the best way to improve the long-run future is to maximize the rate of sustainable economic growth. A similar view is held by many involved in Progress Studies, an intellectual movement that aims to understand and accelerate civilisational progress.
3	An example of an intervention causing a temporary boost in R&D activity would be to fund some researchers for a limited period of time. Another example would be to bring forward in time a policy change that permanently increases the number of researchers.
4	Three comments on the log-utility model. First, the results are the same whatever the values of the constants k and m. Second, I do a sensitivity analysis of the consequences of different utility functions; if the diminishing returns to income are steeper than log, this favours cash transfers more strongly. Third, by expressing the benefits of R&D in terms of their welfare impact I differ from Jones and Summers (2020) who express the benefits in terms of $.
5	log(110) – log(100) ~= 10[log(101) – log(100)] ~= 100[log(100.1) – log(100)] ~= 1000*[log(100.01) – log(100)].
6	More realistically, there will be a lag before productivity benefits are felt. Currently I don’t model this lag because it wouldn’t affect the results by much. I use a discount of 0.2%; so a 50 year lag would reduce the returns to R&D by ~10%.
7	GiveDirectly implements this intervention. Note, I use simplified numbers in this post that don’t exactly match GiveDirectly’s cost effectiveness, and I believe GiveDirectly is somewhat more impactful than the numbers I use imply.
8	Note, rising incomes mean we don’t value adding an equal dollar amount to people’s incomes the same amount through time. We value a dollar more today because people today are poorer than they will be in the future.
9	During the 20th century, the number of researchers grew exponentially, but productivity growth did not increase (in fact it decreased slightly). If R&D is responsible for the productivity growth, then more research effort is required to achieve each subsequent 1% gain in productivity.
10	Note: this does not mean that the absolute $ increase in incomes shrinks over time. It may decline, stay constant or increase, depending on the rate at which ideas are getting harder to find. Technically, if the “fishing out” parameter $ \phi $ > 0, then the absolute $ benefit increases over time. If $ \phi $ < 0, it decreases over time. If $ \phi $ = 0 exactly, it stays constant. I use $ \phi $ = -2.1, estimated in Bloom et al (2020).)
11	The key point is as follows: when ideas are getting harder to find, the number of new ideas found with a marginal researcher-year is roughly proportional to 1 / (total researcher-years so far). So if the 100th researcher-year finds 1/100 new ideas, the 200th researcher-year will find only 1/200 new ideas and the 1000th researcher-year will only find 1/1000 new ideas. Let’s work through the consequences of this point using an example. Suppose an intervention funds an extra researcher-year in 1900, and doesn’t change the amount of research happening in subsequent years. We’ll estimate the impact of the intervention on TFP in 1900 and in 2000. What’s the impact of the intervention on TFP in 1900? Suppose that a total of 100 researcher-years have occurred by 1900. Then the intervention makes the difference between 100 researcher-years vs 101 researchers-years having happened, a difference of 1/100 new ideas. [Here I assume that the number of new ideas found with a marginal researcher-year = 1 / (total researcher-years so far).] 1/100 new ideas correspond to a 0.01% increase in TFP, because we’re defining “an idea” as a 1% TFP increase. What’s the impact of the intervention on TFP in 2000? Suppose that a total of 1000 researcher-years had occurred by 2000. Then the intervention makes the difference between 1000 researcher-years vs 1001 researchers-years having happened, a difference of 1/1000 new ideas. [Here I again assume that the number of new ideas found with a marginal researcher-year = 1 / (total researcher-years so far).] 1/1000 new ideas correspond to a 0.001% increase in TFP. So the intervention raises TFP by 0.01% in 1900, but only by 0.001% in 2000. Its impact on TFP falls towards 0% over time.
12	Mathematically, in the semi-endogenous growth model the effort needed to find a new idea is proportional to TFP^($ \phi $ – 1), where $ \phi $ is the parameter controlling how quickly ideas are getting harder to find. I use $ \phi $ = -1.4, so every time TFP doubles the effort needed to find a new idea increases by 2^2.4 = 5.3.
13	In the long run, there are reasons to think population will fall (fertility rates in developed countries), reasons to think it might increase (relating to biological and cultural evolution), and no compelling reason to think it will stay exactly the same. Still, this feels like a fair ‘default’ case to consider for calculating a stylised value of R&D for our Global Health and Wellbeing team. I discuss some alternative scenarios in appendix E, and list ways the model is optimistic and pessimistic in appendix J.
14	The lag until productivity benefits are felt will probably be larger in low income countries than in high income countries. As mentioned above, I don’t model this lag because it wouldn’t affect the results by much. I use a discount of 0.2%, so a 50 year lag would reduce the returns to R&D by ~10%. Note, the 70% average could arise from <<70% of benefits eventually spilling over to low income countries, and >70% of benefits eventually spilling over to everywhere else. E.g. the poorest half of the global population could get spillovers of 40% while the richest half get spillovers of 100%.
15	In economic growth models, this corresponds to the “stepping on toes” parameter λ = 0.75. I’m not aware of data that pins down λ, and it seems like values between 0.4 and 1 could be correct. I use the estimate from Bloom et al. (2020) Appendix Table A1, where they set λ = 0.75 and then estimate $ \phi $ = -1.4.
16	The primary effect is recorded as a TFP increase because GDP went up holding constant the amount of labour and physical machinery. The secondary effect is recorded as capital deepening because each person has more physical capital (i.e. more or better machinery).
17	Growth theory relates the size of these effects on income: (income increase from TFP and capital deepening) = (income increase from TFP alone) / (1 – capital share of GDP). The capital share is about 35%, so this multiplies the bottom line by 1 / (1 – 0.35) = 1.5.
18	As mentioned in a previous footnote, I think GiveDirectly is somewhat more impactful than the numbers in this row.
19	For example data from Bloom et al. 2020 find the number of US researchers increasing by 4.3% per year on average since 1930. US population grew less than 1.5% per year on average in the same period, implying that the fraction of people doing research was growing.
20	See for example Lee (1988), Kremer (1993), Jones (2001) and Galor and Weil (2000).
21	Though the fraction of people doing research can increase, this can only go on for so long. I discuss this possibility below.
22	There are good theoretical reasons to think TFP can’t grow exponentially at its recent rate for more than 10,000 years, but these don’t rule out exponential growth continuing for another 1000 years.
23	If R&D today expedites a future technology that massively accelerates future growth, the bottom line can increase by much more than 100X. More.
24	My mainline scenario found R&D to be 45% as impactful as giving cash to someone on $500/year. This implies R&D is 4.5% as impactful as our current bar for GHW grantmaking. A 7X increase would leave R&D 31.5% as impactful as the GHW bar.
25	Aghion et al. (2017) discuss the possibility that AI will accelerate productivity growth by automating research tasks.
26	Note, a growth-enhancing technology might allow a constant population of human researchers to maintain ~2% productivity growth, or it might allow them to accelerate productivity growth. Open Philanthropy thinks the latter possibility is more likely than many actors seem to think, for reasons discussed in this report.
27	Of course, growth-enhancing technologies might enable other trends to continue. E.g. the trend of ~2% annual growth in US GDP/capita over the past 150 years, or the trend of growth accelerating over the past 10,000 years.
28	Let’s demonstrate this point with an example. Suppose an intervention causes an extra researcher-year to happen in 2021. Let’s consider its impact on TFP in 2100 if a growth-enhancing technology isn’t developed, and if it is developed. Suppose that if a growth-enhancing technology isn’t developed then a total of 1000 researcher-years will have happened by 2100. Then the intervention makes the difference between 1000 researcher-years vs 1001 researcher-years having happened, a difference of 1/1000 new ideas. [Here I assume that the number of new ideas found with a marginal researcher-year = 1 / (total researcher-years so far). This is a consequence of ideas getting harder to find.] If a growth-enhancing technology is developed, then a total of 9000 researcher-years will have happened by 2100. Then the intervention makes the difference between a 9000 researcher-years vs 9001 researchers-years having happened, a difference of 1/9000 new ideas. [Here I assume that the number of new ideas found with a marginal researcher-year = 1 / (total researcher-years so far).] So the intervention causes 1/1000 new ideas in 2100 if a growth-enhancing technology isn’t developed, but only 1/9000 new ideas if it is developed. Note: I assume that the intervention doesn’t change the amount of research done in later years, so it always makes a difference of 1 researcher-year. But if the intervention brought the growth-enhancing technology forward in time, it would increase the amount of research in later years. This would significantly change the calculation.
29	Appendix D does a very rough BOTEC on the returns to R&D for one possible growth-enhancing technology.
30	Eg. see this draft report by Joe Carlsmith on risk from power-seeking AI, or these two posts from the Cold Takes blog.
31	Even if R&D isn’t competitive according to either worldview, might it look competitive according to a weighted sum of both? I think not. I estimate funding generic R&D to be ~10X worse than the GHW bar, and it looks significantly worse from a LTist perspective than alternative interventions.
32	Appendix H discusses some potential differences between my perspective and that of Progress Studies advocates.
33	The simulation assumes that the increase in R&D activity is proportional to the increase in funding. This may be optimistic: in reality you need both funding and researchers to do R&D. Essentially, the simulation assumes that more funding will bring with it more researchers, which may be optimistic.
34	So it ignores the additional effect that capital deepening has on TFP increases in standard growth models.
35	It assumes everyone is on the world average income. Representing income inequality wouldn’t change the results. This is because we ultimately care about the percentage effect of R&D on income, and this is the same no matter what people’s starting incomes are. We care about the percentage effect because we assume utility = k + m*ln(income).
36	The specific values used for k and m do not affect the result as they cancel. In practice we use k=0 and m=1.
37	It quantifies the result in this way because this is a metric Open Philanthropy uses internally to compare the impacts from different kinds of intervention.
38	More precisely, the absolute size of the annual increment is 2% of current research intensity: 0.02 * 2.3% = 0.046%. So this assumption corresponds to thinking that research intensity has been growing exponentially at about 2% per year, but this exponential rate of increase will decline over time.
39	See page 20 of Jones and Summers (2020).
40	How long does it take for the “wedge declines more slowly” effect to dominate if we have no discount? Let’s assume we change our value of $ \phi $ to compensate when we change lambda. How long does it take for the total impact from $ \lambda $=0.75 to exceed the impact from $ \lambda $=1? With constant exponential population growth of 1% it takes ~250 years. With population stagnating after 80 years, it takes ~5000 years. If we held $ \phi $ constant when changing lambda, or used a discount, it would take longer (perhaps never) for the impact from $ \lambda $=0.75 to exceed the impact from $ \lambda $=1.
41	I get this expression by differentiating the expression for $ g_A $ with respect to $ L $: $ wedge = d(g_A)/dL $.
42	Why would this happen? We caused some extra counterfactual science to happen: R(t)+1 researcher-years rather than R(t) at each time t. But this extra science makes less % difference to income as ideas become harder to find. 100 vs 101 researcher-years makes a bigger % difference to income than 1000 vs 1001.
43	The wedge halves each time researcher population doubles (assuming the ‘stepping on toes’ parameter $ \lambda $=1). The relationship between TFP growth g and population growth n in steady state is given by g = $ \lambda $ * n / (1 – phi). Using $ \lambda $=1 and $ \phi $=-2 (values from Bloom et al. 2020) implies g = n/3. Researcher population growth is 3X faster than TFP growth. By the time TFP has grown 30%, population has ~doubled and to the wedge has ~halved.
44	See Bostrom (2003) for a slightly more detailed explanation of this point.
45	This is exactly true in the semi-endogenous framework when the “stepping on toes” parameter lambda=1. If lambda < 1 then the population more than doubles each time the wedge halves.
46	Here’s another way to understand this effect. Because ideas are getting harder to find, the number of new ideas found with a marginal researcher-year is roughly proportional to 1 / (total years of research so far). Suppose we fund an extra year of research in 2021. As a result, in 2050 one more researcher-year has occurred. The number of ideas found with this extra researcher-year is proportional to 1 / (total years of research by 2050). If the fraction of people doing R&D increases, this quantity will be smaller.
47	See Bloom et al (2020) and https://mattsclancy.substack.com/p/innovation-gets-mostly-harder.
48	101 researchers working for 1 year make the same amount of progress as 100 researchers working for (1 + 1/100) years.
49	Another way to think about this is that we assume that the total R&D effort at each time is determined by the level of technology. I.e. the level of technology determines both the population and the research concentration and so determines the total R&D effort. So if we reach a given level of technology x years earlier, we also reach the corresponding level of R&D effort x years earlier. Again, this assumption captures the idea that R&D in 1800 increased the amount of R&D at later times.
50	See data from Roodman (2020).
51	You need ~27 10% income increases to go from $700 to $9600. So you need 27 billion 10% income increases to raise 1 billion people’s income from $700 to $9600. Here I use the fact that all 10% income increases are valued equally, which comes from the log-utility model. 1.1^23 = 14 = 9600 / 700.
52	The assumption that researchers earn the average global wage, rather than a higher wage, will make no difference to the result. This is because I will make an equivalent assumption about the wages of researchers in 2020. The results would change somewhat if you think researchers today demand more (or less) of the premium than researchers in 1800.
53	For consistency with the 1800 calculation (see most recent fn), I assume that 1 researcher-year costs the same as the global average income. Today that is about $10,000. The model for R&D today implies that $100 to R&D has the same welfare effect as raising someone’s income by 7% for one year. So $10,000 has the same effect as raising 100 people’s incomes by 7%. Given the log-utility model, this is roughly the same welfare effect as raising 70 people’s incomes by 10%.
54	1.028^90 = 12.
55	1.016^130 = 8
56	1.008^130 = 3.
57	See Bloom et al. (2013), Coe and Helpman (1995) and references within Jones and Williams (1998) and Jones and Summers (2020).
58	0.75*0.4%/2.3% = 0.13.
59	E.g. Bloom et al. (2013) estimate a private return of 21% and a social return of 55%. See multiple estimates in table 1 of Jones and Williams (1998) and in Appendix B of Jones and Summers (2020).
60	Conversely, if I’d used the depreciation assumptions used in the empirical estimates, I’d have expected the benefit from marginal R&D to diminish much more quickly over time and calculated a lower total return to R&D.
61	The model here differs from the standard semi-endogenous growth model in two ways. First, the standard semi-endogenous growth model assumes that all TFP growth is due to R&D; this model relaxes this assumption. Second, this model translates income changes to welfare changes using a log-utility model.
62	E.g. see Patrick Collison here, 19:57-25:32.
63	I.e. as income falls, the marginal utility of income increases by more.
64	https://ourworldindata.org/grapher/gdp-per-capita-worldbank?tab=chart&yScale=log&country=OWID_WRL~USA Imagine someone in 1990 who earns $40k being offered the following choice:
65	To make the comparison fair, in option 2 you should be forced to buy all goods and services at 2020 prices. This means that some services will be more expensive than in 1990. Even so, I think option 2 is better because there are many new products that are cheap but useful. If this doesn’t seem right, you might consider a more extreme version of the thought experiment. Instead of comparing 2020 with 1990, compare 2020 with 990. Imagine offering a medieval peasant enough medieval goods and services — food, land, servants — that their income is $60k a year. Would they prefer that, or being on $60k in 2020 with the conveniences of central heating, clean running water, varied food, modern medicine, etc? Here it seems clear to me that the latter option is better.
66	How much does the income increase underestimate the welfare benefit of technological progress? You could roughly estimate this by increasing the cash payment in option 1. E.g. suppose you’re indifferent between option 2 and option 1’) A cash payment of $40k. This would imply that the true welfare benefit is very roughly 2X the income increase. (This is very rough because the utility gains from receiving $40k are not twice those from $20k, due to diminishing returns to $.)
67	Phil Trammell describes one such utility function here. Also see discussion by Matt Clancy in the “What about other benefits?” section of this post.

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.

Social Returns to Productivity Growth

Table of Contents

Intro

My estimate of the social returns to R&D

Toy Example

A more realistic calculation

Bottom line – social returns to R&D

The best pro-growth interventions are better than average R&D

Funding R&D was even better in the past

Limitations of the model

The model ignores potential harms from R&D

The model implies growth will stagnate

Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find?

Other limitations of the model

How significant are these limitations?

Conclusion

Description of the appendices

Appendix A: Assumptions of the model

Simulation assumptions

What model of R&D am I using?

How do I apply this model in the simulation?

Other simulation assumptions

Adjustments made to simulation output

Expressing the benefit in terms of a % income increase

Substantive adjustments

What proportion of productivity benefits should we credit to R&D?

Full list of assumptions

Appendix B: understanding the implications of semi-endogenous growth for the social returns to R&D

What’s the initial size of TFP wedge?

How does the TFP wedge change over time?

Appendix C: deriving quantitative implications of semi-endogenous models for returns to R&D

What’s the initial size of wedge?

How does the wedge change over time?

Appendix D: very rough estimates of the social returns to R&D under different scenarios

Mainline scenario: Ideas getting harder to find and stagnating population drive productivity stagnation.

Maybe we’ll avoid productivity stagnation by increasing the fraction of people doing R&D?

Maybe ideas won’t get harder to find in the future?

Maybe some trend-breaking future technology will allow us to avoid growth stagnation despite ideas getting harder to find?

Maybe the world’s population won’t stagnate?

Appendix E: reasons growth might not stagnate, and how that would affect the bottom line

Maybe we’ll avoid stagnating growth by increasing the fraction of people doing R&D?

Maybe ideas won’t get harder to find in the future?

Maybe the world’s population won’t stagnate?

Appendix F: back-of-the-envelope calculations of value of R&D in 1800

Explaining the model

Applying the model

Data on the research concentration in 1800

Appendix G: top-down vs bottom-up calculations of the returns to R&D

Summary

Top-down vs bottom-up calculations of R&D returns

Using bottom-up approaches to calibrate the assumptions of the model in this post

Appendix H: Potential disagreements with Progress Studies

Appendix J: ways in which the stylized estimate is too pessimistic vs too optimistic

Arguably too optimistic

Arguably too pessimistic

Appendix K: additional limitations of the model

The model assumes research today doesn’t change the amount of research tomorrow

Uncertainty about the utility function